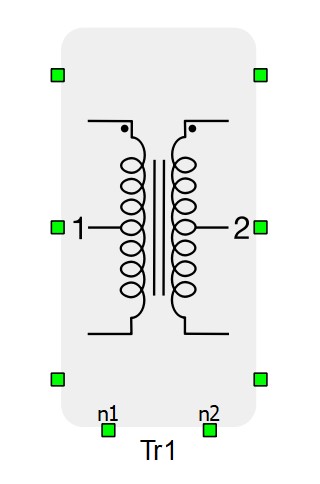
Three Phase Two Winding Transformer

Three Phase Two Winding Transformer is modeled as three single-phase transformers, meaning that only magnetic coupling between windings of the same phase are taken into account. The magnetization inductance Lm can be linear or with saturation, it is modeled on the primary side of the transformer. Core losses are modeled as Rm resistance located on the primary side of the transformer. Also, it is possible to neglect Lm and Rm by selecting Lm/Rm neglected in the Core model property. Finally, Hysteresis can also be simulated for slower dynamics. For more information, please refer to the Core model section.

Measurement results obtained from these tests and other information given on the transformer’s nameplate provide the necessary data for transformer characterization and modeling.

Winding excitation in the tests is three-phase positive sequence voltage. In addition to that, when characterizing a transformer and making a transformer model that includes mutual inductances between phases, it is necessary to perform the same tests, but with excitation being three-phase zero sequence voltage.

Parameters of the equivalent circuit are calculated as follows. During the short circuit test, the magnetization branch is considered shorted by the short circuited winding. So, primary side short circuit impedance is obtained by:

Primary side short circuit resistance is obtained by:

Primary side short circuit inductance is obtained by:

Primary and secondary side resistances and short circuit inductances are calculated using:

$R_1=\frac{1}{2}{R}_{sc}$

$R_2=\frac{1}{2}{R}_{sc}{\left(\frac{N_2}{N_1}\right)}^2$

$L_1^d=\frac{1}{2}{L}_{sc}^d$

$L_2^d=\frac{1}{2}{L}_{sc}^d{\left(\frac{N_2}{N_1}\right)}^2$

From the positive sequence open circuit test results, it is obtained:

$i_{oc}^d=\frac{i_{oc}^d\left[\%\right]}{100}{I}_{1n}^{ph}=i_{oc}^d\left[\%\right]\frac{S_n}{300V_{1n}^{ph}}$

$P_{oc}^d=3\frac{{\left(V_{1n}^{ph}\right)}^2}{R_{Fe}^d}\stackrel{yields}{\to }{R}_{Fe}^d=3\frac{{\left(V_{1n}^{ph}\right)}^2}{P_{oc}^d}$

$P_{oc}^d=3R_{Fe}^d{\left(i_{Fe}^d\right)}^2\stackrel{yields}{\to }{\left(i_{Fe}^d\right)}^2=\frac{P_{oc}^d}{3R_{Fe}^d}$

$i_m^d=\sqrt{{\left(i_{oc}^d\right)}^2-{\left(i_{Fe}^d\right)}^2}$

$L_m^d=\frac{1}{2\pi f_n}\frac{V_{1n}^{ph}}{i_m^d}$

A schematic block diagram of the three-phase two-winding transformer block with the corresponding component arrangement and naming is shown in Figure 2.

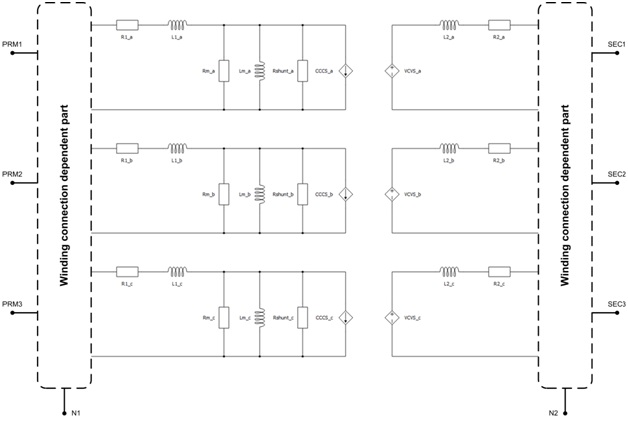
It should be noted that terminals N1 and N2 can be connected with the rest of the circuit in Schematic Editor only if the corresponding side is wye (Y) connected.

Embedded coupling

There are two possible options for embedded coupling in Three Phase Two Winding Transformer: Ideal Transformer based coupling and TLM coupling.

• Ideal Transformer Embedded coupling type is ignored in TyphoonSim and will not affect TyphoonSim simulation at all.
• TLM Embedded coupling type will be replaced with a corresponding inductor in TyphoonSim.

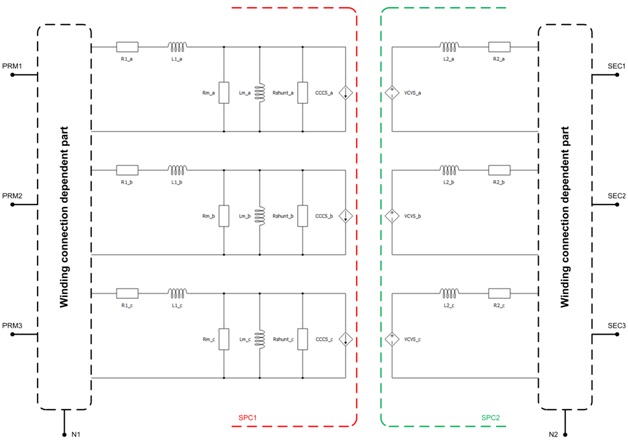
If Embedded coupling is Ideal Transformer, Ideal Transformer based coupling will be placed between the two windings of the transformer.

Figure 3 gives a visual representation of the division of transformer's equivalent circuit in the case where Embedded coupling is set to Ideal Transformer.

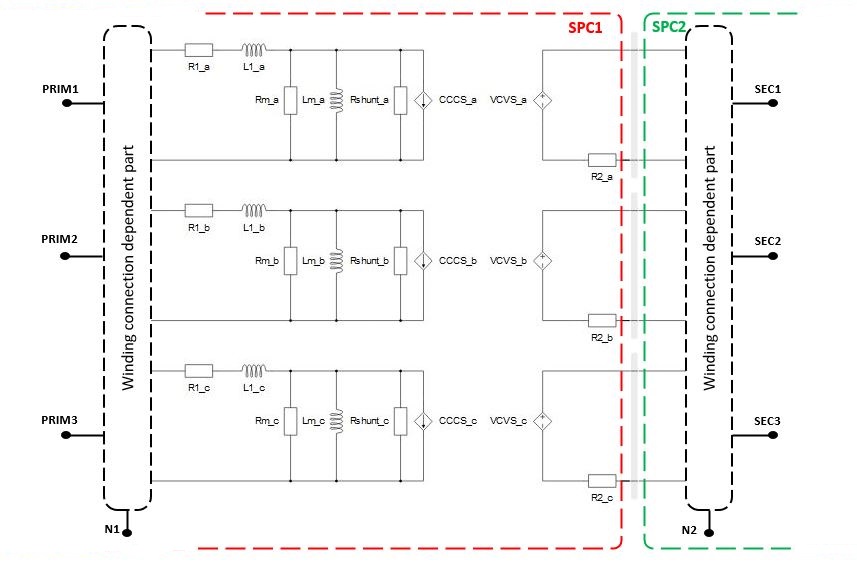
If Embedded coupling is set to TLM, the secondary winding inductor in the each phase will be replaced with a TLM coupling component. Inductance will be divided between coupling and embedded inductors (inductors will be hidden in the TLM). The TLM to embedded inductors ratio can be determined by the compiler, but it can also be specified explicitly. If the Automatic option is selected, the ratio will be determined by the discretization method. If the Manual option is selected, the ratio can be explicitly set to meet user requirements. For more information on TLM couplings please refer to Core couplings - TLM.

Figure 4 gives a schematic representation of the transformer's equivalent circuit when Embedded coupling is set to TLM.

Ports

• prm_1 (electrical)
  • Primary winding port 1.

• prm_2 (electrical)
  • Primary winding port 2.

• prm_3 (electrical)
  • Primary winding port 3.

• n1 (electrical)
  • Available if Winding 1 connection is set to Y
  • Primary winding neutral port.

• sec_1 (electrical)
  • Secondary winding port 1.

• sec_2 (electrical)
  • Secondary winding port 2.

• sec_3 (electrical)
  • Secondary winding port 3.

• n2 (electrical)
  • Available if Winding 2 connection is set to Y
  • Secondary winding neutral port.
• prm_1_2 (electrical)
  • Available if Winding 1 connection is set to O
  • Primary winding port 2.
• prm_2_1 (electrical)
  • Available if Winding 1 connection is set to O
  • Primary winding port 3.
• prm_2_2 (electrical)
  • Available if Winding 1 connection is set to O
  • Primary winding port 4.
• prm_3_1 (electrical)
  • Available if Winding 1 connection is set to O
  • Primary winding port 5.
• prm_3_2 (electrical)
  • Available if Winding 1 connection is set to O
  • Primary winding port 6.
• sec_1_2 (electrical)
  • Available if Winding 2 connection is set to O
  • Secondary winding port 2.
• sec_2_1 (electrical)
  • Available if Winding 2 connection is set to O
  • Secondary winding port 3.
• sec_2_2 (electrical)
  • Available if Winding 2 connection is set to O
  • Secondary winding port 4.
• sec_3_1 (electrical)
  • Available if Winding 2 connection is set to O
  • Secondary winding port 5.
• sec_3_2 (electrical)
  • Available if Winding 2 connection is set to O
  • Secondary winding port 6.

General (Tab)

• Input parameters
  • Specifies parameters format (SI, pu, or SC and OC tests).
• Sn
  • Available if Input parameters is set to pu or SC and OC tests.
  • Nominal Power of the transformer [VA].
• f
  • Available if Input parameters is set to pu or SC and OC tests.
  • Nominal frequency [Hz].

• Flux values
  • Available if Core model is set to Non-Linear or to Hysteresis.
  • List of magnetic flux values [Wb] or [pu].

• Current values
  • Available if Core model is set to Non-Linear or to Hysteresis.
  • List of current values [A] or [pu].
• Hysteresis flux values
  • Available if Core model is set to Hysteresis
  • Vector of mgnetizing flux for upper hysteresis [Wb] or [pu]
• Rm
  • Available if Input parameters is set to SI and Core model is set to Linear, Non-Linear, or Hysteresis.
  • Resistance representing core losses [Ω].
• Lm
  • Available if Input parameters is set to SI and Core model is set to Linear.
  • Magnetization inductance [H].
• ioc1
  • Available if Input parameters is set to SC and OC tests and Core model is set to Linear, Non-Linear, or Hysteresis.
  • Postive sequence no load excitation current
• Poc1
  • Available if Input parameters is set to SC and OC tests and Core model is set to Linear, Non-Linear, or Hysteresis.
  • Postive sequence no load losses
• Execution rate
  • Available if Core model is set to Hysteresis.
  • Defines the execution rate of measurement and signal processing components.

Winding connection (Tab)

• Winding 1 connection

  • The available connections are star (Y), delta (D), and open winding (O).

• Winding 2 connection

  • The available connections are star (Y), delta (D), and open winding (O).

• Clock number
  • Available if Winding 2 connection is set to D or Y and Winding 1 connection is set to D or Y.
  • Determines the phase displacement between primary and secondary side voltages

Coupling (Tab)

• Ideal Transformer Embedded coupling type is ignored in TyphoonSim and will not affect TyphoonSim simulation at all.
• TLM Embedded coupling type will be replaced with a corresponding inductor in TyphoonSim.