Fuel Cell

PEM Fuel Cell modeling

The hydrogen fuel cell component is implemented using a signal controlled voltage source, a current measurement, and a fuel cell signal processing model as seen in Figure 2. The proton exchange membrane fuel cell in particular is known to have slower reaction kinetics at the cathode side (air) than at the anode side (hydrogen). As consequence, the cathode activation loss is an order of magnitude higher than the anode activation loss. In this PEM fuel cell model, the anode side activation loss effects are neglected for the sake of simplification purposes.

Figure 2. Schematic diagram of fuel cell model

Considering this, the PEM fuel cell stack output terminal voltage can be expressed by the following equations:

$V_{s t a c k} = {N_{c e l l} ∙ V}_{c e l l}$

$V_{c e l l} = E_{c e l l} - V_{o h m} - V_{a c t}$

where $E_{c e l l}$ is the thermodynamic voltage of the fuel cell, $V_{o h m}$ is the voltage drop on the electrolyte ionic resistance and $V_{a c t}$ is the cathode activation losses voltage.

Thermodynamic voltage of the PEM fuel cell can be modeled from the Nernst equation:

$E_{c e l l} = 1.229 - 0.85 ∙ 10^{- 3} (T_{c e l l} - 298.15) + \frac{R ∙ T_{c e l l}}{2 F} \ln (P_{H_{2} c a t a} ∙ \sqrt{P_{O_{2} c a t a}})$

where $T_{c e l l}$ is the temperature of the cell in Kelvins, $P_{O_{2} c a t a}$ is the oxygen pressure at the cathode catalytic interface in atm, $P_{H_{2} c a t a}$ is the hydrogen pressure at the anode catalytic interface in atm, R=8.314 is the universal gas constant in J/(mol·K), and F=96485.3 is the Faraday constant in C/mol.

The differences between the gas supply pressures and the catalyst interface pressures (effective gas pressure for electrochemical reactions) are due to the gas diffusion phenomenon through the porous electrodes in a PEM fuel cell, which can be modeled by Fick's law:

$P_{x c a t a} = P_{x} - \frac{N_{x} ∙ δ_{G D L} ∙ R ∙ T_{c e l l}}{D_{x - H_{2} O e f f} ∙ A_{M E A}} x \in (H 2, O 2)$

where $δ_{G D L}$ is the gas diffusion layer thickness, $D_{x - H_{2} O e f f}$ is the effective gas diffusion coefficient, and the reactant gas (hydrogen and oxygen) molar flow rates are directly related to the fuel cell current i:

$N_{H_{2}} = \frac{i}{2 ∙ F}$

$N_{O_{2}} = \frac{i}{4 ∙ F}$

The effective gas diffusion coefficients $D_{x - H_{2} O e f f}$ , can be obtained from the binary gas diffusion coefficient and the Bruggemann correction term for the porous electrode of the fuel cell:

$D_{x - H_{2} O e f f} = D_{x - H_{2} O} ∙ ε^{τ} x \in (H 2, O 2)$

where $D_{x - H_{2} O}$ is the binary gas diffusion coefficient in m²/s, between the reactants $H_{2}$ , $O_{2}$ and product $H_{2} O$ , ε is the corresponding gas diffusion layer porosity, and $τ$ is the corresponding gas diffusion layer tortuosity.

Cathode activation losses voltage can be modeled using the following differential equation:

$\frac{d}{d t} V_{a c t} = \frac{i}{C_{d l}} (1 - \frac{1}{η_{a c t}} V_{a c t})$

where $C_{d l}$ is the single fuel cell cathode double layer capacitance in Farads, i is the fuel cell current in Amperes, and $η_{a c t}$ is the cathode steady-state activation loss value, calculated using the well-known Tafel equation:

$η_{a c t} = \frac{R ∙ T_{c e l l}}{2 ∙ α ∙ F} \ln (\frac{i}{j_{0,C} ∙ A_{M E A}})$

where $α$ is the electrochemical reaction symmetry factor (usually between 0.2 and 0.5), $A_{M E A}$ is the Membrane Electrode Assembly geometric surface area of a single cell in m², and $j_{0,C}$ is the cathode exchange current density in A/m², calculated by the following empirical equation:

$j_{0,C} = γ ∙ P_{O_{2} c a t a}^{β} ∙ e^{- \frac{E_{c}}{R ∙ T_{c e l l}} (1 - \frac{T_{c e l l}}{298.15})}$

where $γ$ and $β$ are two empirical parameters that need to be identified through fuel cell experimental tests, and $E_{c}$ is the constant representing oxygen activation energy at electrode platinum interface (66000 J/mol).

Note: The Fuel Cell component can be switched between dynamic cathode activation losses voltage calculation as

V_{a c t}

, or steady-state activation losses voltage as

η_{a c t}

by changing the combo box Double layer capacitance dynamics, as seen in the Electrochemical characteristic (Tab).

Note: Because the cathode activation loss of the fuel cell is modeled by the explicit Tafel equation, the model results might be less accurate than experimental ones when electrical current value is very close to zero. To accurately calculate cathode activation loss for extremely small current values, the full Butler-Volmer equation in its implicit form should be used.

Electrolyte ionic resistance voltage drop can be calculated from the membrane resistance:

$V_{o h m} = i ∙ R_{m e m}$ and $R_{m e m} = \frac{δ_{m e m}}{σ_{m e m} ∙ A_{M E A}}$

where $δ_{m e m}$ is the PEM thickness, and $σ_{m e m}$ (S/m) is the proton conductivity of a Nafion type polymer membrane, which is highly related to the water content of the membrane. Its value can be calculated by:

$σ_{m e m} = (0.5139 ∙ λ_{m e m} - 0.326) ∙ e^{[1268 (\frac{1}{303} - \frac{1}{T_{c e l l}})]}$

where

λ_{m e m}

is the membrane water content:

λ_{m e m} \approx 7

for a dry membrane,

λ_{m e m} \approx 14

for a well-humidified membrane and

λ_{m e m} \approx 22

for a flooded membrane.

Note: The polymer membrane proton conductivity model is applied for Nafion-type materials only.

Thermal calculation:

The fuel cell's energy balance can be calculated by considering the various energy terms (sources, sinks, etc.) during fuel cell operation:

$Q_{c o o l i n g} = h A ∙ (T_{c e l l} - T_{c o o l i n g})$

$Q_{t h e o} = \frac{i}{2 ∙ F} Δ H$

$Q_{e l e c} = i ∙ V_{c e l l}$

where $Q_{c o o l i n g}$ is the heat removal rate from a single fuel cell by the cooling circuit (either forced cooling or natural cooling) in J/s, $Q_{t h e o}$ is the total theoretical thermodynamic power produced during the electrochemical reaction in J/s, $Δ H$ is the hydrogen-oxygen reaction enthalpy change in the fuel cell at a higher heating value (286 kJ/mol with liquid water as product), and $Q_{e l e c}$ is the fuel cell total output electrical power (W).

Using the heat transfer formula, cell temperature can be calculated with:

$M ∙ C_{p} ∙ (\frac{d T_{c e l l}}{d t}) = Q_{t h e o} - Q_{e l e c} - Q_{c o o l i n g}$

where hA is the cooling coefficient in W/K, Cp is the equivalent thermal capacity of the fuel cell in J/(kg*K), M is the mass of the fuel cell in kg, and $T_{c o o l i n g}$ is the ambient temperature in Kelvins.

Note: The Fuel Cell component has can be switched between temperature calculation and constant temperature by changing the checkbox Temperature model type, as seen in the Thermal model (Tab).

General (Tab)

N cell
- Number of fuel cells per fuel cell stack (connected in series)
- The parameter scales the output voltage by the number of fuel cells without any additional effects.
Execution rate
- Signal processing execution rate of the fuel cell component.
Signal outputs
- Enables/disables signal processing outputs. When enabled, a signal output port appears on the component.
- Available outputs are in the following order:
  1. Temperature of the fuel cell(s)
  2. Terminal output voltage of the fuel cell stack
  3. Terminal fuel cell current
  4. Output voltage of a single fuel cell

Electrochemical characteristic (Tab)

Double layer capacitance dynamics
- Enables/disables activation layer voltage using the double layer capacitance dynamics
- When enabled, $\frac{d}{d t} V_{a c t} = \frac{i}{C_{d l}} (1 - \frac{1}{η_{a c t}} V_{a c t})$ , where $V_{a c t}$ is the activation layer voltage, and $η_{a c t}$ is the cathode steady-state activation loss.
- When disabled, $V_{a c t}$ is equal to $η_{a c t}$
C dl
- Available if Double layer capacitance dynamics is enabled
- Single fuel cell double layer capacitance
Alpha constant
- Electrochemical reaction symmetry factor (usually between 0.2 and 0.5)
Beta constant
- Affects exchange current density of cathode electrode and the value of cathode activation loss (needs to be determined empiricaly)
Gamma constant
- Affects exchange current density of cathode electrode and the value of cathode activation loss (needs to be determined empiricaly)

Fluidic coefficients (Tab)

D O2-H2O
- Binary oxygen gas to vapor diffusion coefficient
D H2-H2O
- Binary hydrogen gas to vapor diffusion coefficient

Fuel cell geometry (Tab)

Eta GDL
- The gas diffusion layer porosity, which is used to calculate the effective gas diffusion coefficient in the fuel cell porous electrode
Tau GDL
- The gas diffusion layer tortuosity, which is used to calculate the effective gas diffusion coefficient in the fuel cell porous electrode
Delta GDL
- The gas diffusion layer thickness
A MEA
- The Membrane Electrode Assembly (MEA) surface area of a single fuel cell (this property represents the geometric surface area and not the effective surface area of the catalyst)
Delta MEM
- The proton exchange membrane thickness

Thermal model (Tab)

Temperature model type
- Specifies the temperature model type
- Available values are Static model and Dynamic model
- Static model forces the temperature of the fuel cell to be constant and equal to Tcell
- Dynamic model enables heat transfer equations and calculates temperature based on cooling inlet/ambient temperature Tcooling, thermal model parameters, and fuel cell conditions
Tcell
- Available if Temperature model type is set to Static model
- Fuel cell temperature [K]
- The entered value is kept constant during the simulation
Tcooling
- Available if Temperature model type is set to Dynamic model
- The cooling inlet temperature (for forced cooling) or the ambient temperature (for natural cooling) [K]
Cp
- Available if Temperature model type is set to Dynamic model
- Equivalent thermal capacity of a single fuel cell's materials [J/(kgK)]
hA
- Available if Temperature model type is set to Dynamic model
- The cooling coefficient (forced or natural) of the fuel cell (a product of the heat transfer coefficient in W/(m²*K) and the cell’s effective cooling surface in m²)
- In the case of forced cooling the heat transfer coefficient is the fluid-solid surface's forced heat transfer coefficient of the coolant (water or air in most cases). The effective cooling surface is the total contact surface area of cooling channels
- In the case of natural cooling the heat transfer coefficient is the surface's natural heat transfer coefficient of air and the effective cooling surface is the external surface area of fuel cell stack exposed to ambient air
M
- Available if Temperature model type is set to Dynamic model
- The mass of a single fuel cell [kg]

Note: The Fuel Cell parameters Cp, hA, and M can be entered for the fuel cell stack as well as for a single fuel cell. It is important however that all three parameters together reference only one of these two options.

Operating conditions (Tab)

P H2
- Hydrogen gas supply pressure of the fuel cell [atm]
P O2
- Oxygen gas supply pressure of the fuel cell [atm]
- If supplied by air, a coefficient of 21% should be used, representing the O₂ molar fraction in air
Lambda mem
- Membrane water content

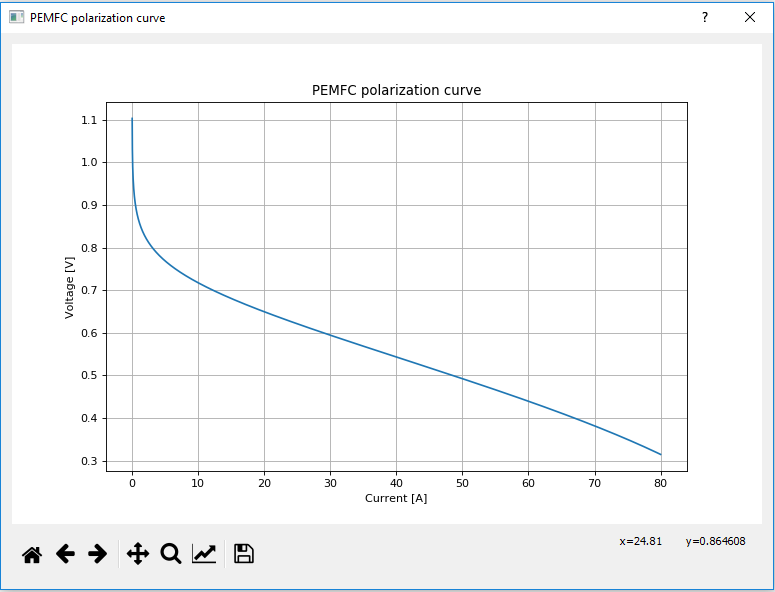
Polarization curve (Tab)

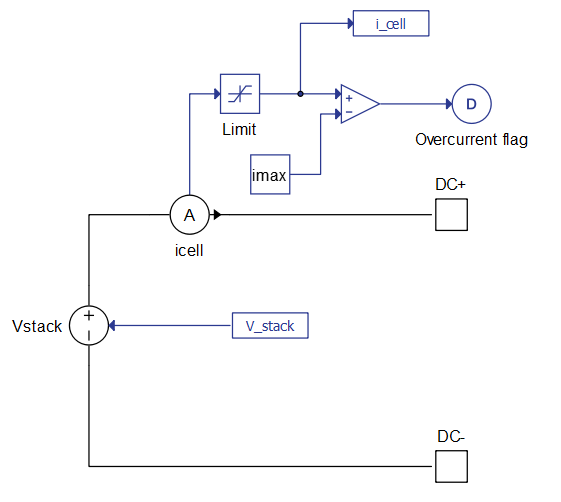
Imax
- The maximum current of the polarization curve [A]
- If during the simulation, the terminal current of the fuel cell component increases beyond this value an overcurrent flag will be raised to 1. This signal measurement is located inside the specific fuel cell component and it is always enabled. If the terminal fuel cell current drops below the Imax value, overcurrent flag will again return to 0

The fuel cell's static characteristics are represented by its polarization curve. This curve shows the output voltage of a single fuel cell as function of its current when the Preview Polarization Curve button is clicked.