Three Phase Permanent Magnet Synchronous Machine
Description of the Three Phase Permanent Magnet Synchronous Machine component in Schematic Editor.
A, B, and C are stator winding terminals. The stator winding uses the current source interface.
Electrical sub-system model
The electrical part of the machine is represented by the following system of equations, modeled in the rotating dq reference frame. The dq reference frame is attached to the rotor, and the direct axis is aligned with the rotor magnets. The modeled dynamics can be represented with the following equations:
If the saturation effects are considered, the equations have the same form, but in that case fluxes are functions of stator currents:
Additionaly, if the saturation effects are considered, the permanent magnet flux may also be a function of stator currents:
If the saturation effects and machine's flux and torque spatial harmonics are considered, the equations also have the same form, but in that case fluxes are functions of the rotor mechanical angle and stator currents:
| symbol | description |
|---|---|
| ψds | Direct axis component of the stator flux [Wb] |
| ψqs | Quadrature axis component of the stator flux [Wb] |
| ψPM | Flux amplitude established in stator phases by rotor permanent magnets [Wb] |
| ids | Direct axis component of the stator current [A] |
| iqs | Quadrature axis component of the stator current [A] |
| vds | Direct axis component of the stator voltage [V] |
| vqs | Quadrature axis component of the stator voltage [V] |
| Rs | Stator phase resistance [Ω] |
| Ld | Direct axis inductance [H] |
| Lq | Quadrature axis inductance [H] |
| ωr | Rotor electrical speed [rad/s] ( ) |
| p | Machine number of pole pairs |
| Te | Machine developed electromagnetic torque [Nm] |
| θm | Rotor mechanical angle [rad] |
Mechanical sub-system model
Motion equation:
| Symbol | Description |
|---|---|
| ωm | Rotor mechanical speed [rad/s] |
| Jm | Combined rotor and load moment of inertia [kgm2] |
| Te | Machine developed electromagnetic torque [Nm] |
| Tl | Shaft mechanical load torque [Nm] |
| b | Machine viscous friction coefficient [Nms] |
| θm | Rotor mechanical angle [rad] |
Saturation effects
The permanent magnet synchronous machine model can include magnetic saturation effects. In that case, fluxes or inductances are defined as functions of stator currents ids and iqs. These functions are represented in the form of lookup tables. The lookup tables use linear interpolation and linear extrapolation.
- fluxes vs stator currents
- absolute inductances vs stator currents
- incremental inductances vs stator currents
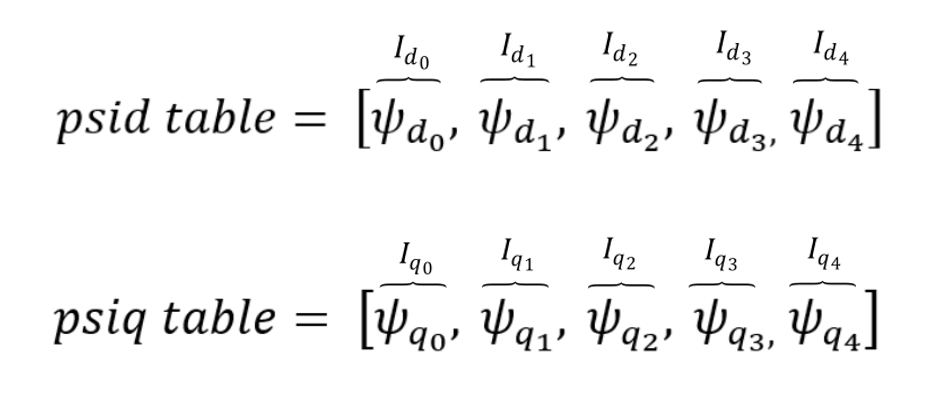
id_vector = [-40.0, -20.0, 0.0, 20.0, 40.0]
iq_vector = [-40.0, -20.0, 0.0, 20.0, 40.0]
psid_table = [-0.0492472, -0.0433668, -0.0425532, -0.0433464, -0.0484104]
psiq_table = [-0.1330824, -0.0838922, 0.0, 0.0838828, 0.133098]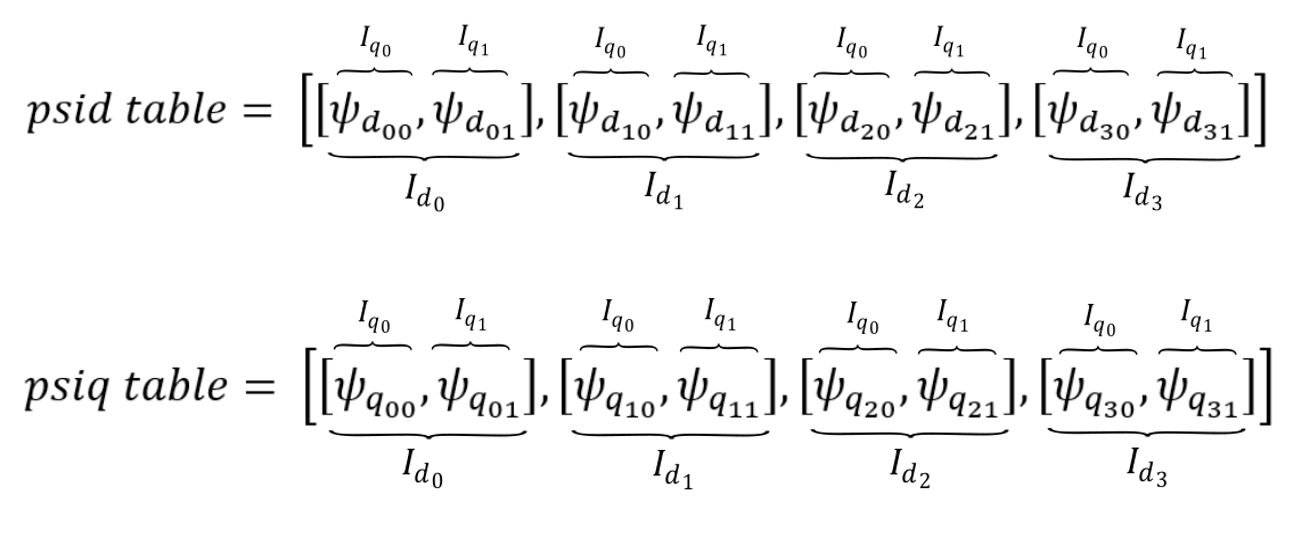
id_vector = [-40.0, -20.0, 0.0, 20.0, 40.0]
iq_vector = [-40.0, -20.0, 0.0, 20.0, 40.0]
psid_table = [[-0.0492472, -0.0433668, -0.0425532, -0.0433464, -0.0484104],
[-0.0115952, -0.0274476, -0.0330376, -0.02771, -0.0126918],
[0.032, 0.032, 0.032, 0.032, 0.032],
[0.064706, 0.0662274, 0.0593586, 0.0677826, 0.0649068],
[0.0805368, 0.0705448, 0.05448328, 0.070713, 0.0812716]]
psiq_table = [[-0.1330824, -0.0838922, 0.0, 0.0838828, 0.133098],
[-0.1313616, -0.1041012, 0.0, 0.1041148, 0.1282268],
[-0.1286288, -0.1076058, 0.0, 0.107, 0.1278272],
[-0.1175936, -0.084391, 0.0, 0.0839394, 0.1162836],
[-0.1092448, -0.0588548, 0.0, 0.0585804, 0.1084576]]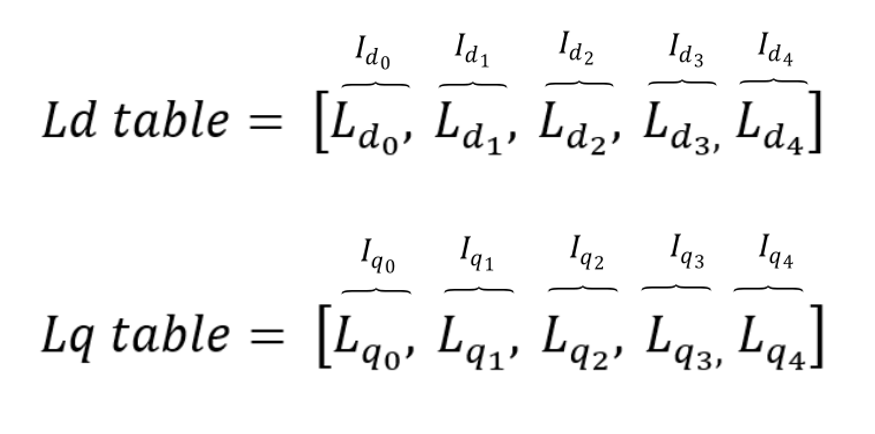
id_vector = [-40.0, -20.0, 0.0, 20.0, 40.0]
iq_vector = [-40.0, -20.0, 0.0, 20.0, 40.0]
Ld_table = [0.00186383, 0.00325188, 0.00399657, 0.00136793, 0.000562082]
Lq_table = [0.00321572, 0.00538029, 0.00779154, 0.00535, 0.00319568]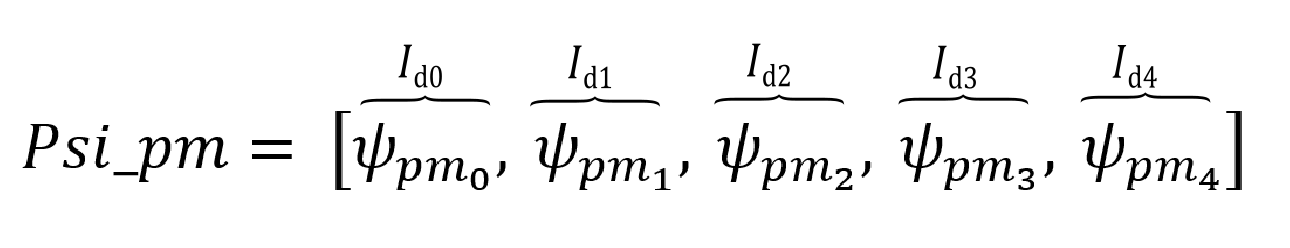
Psi_pm = [0.0492472, 0.0433668, 0.0425532, 0.0433464, 0.0484104]
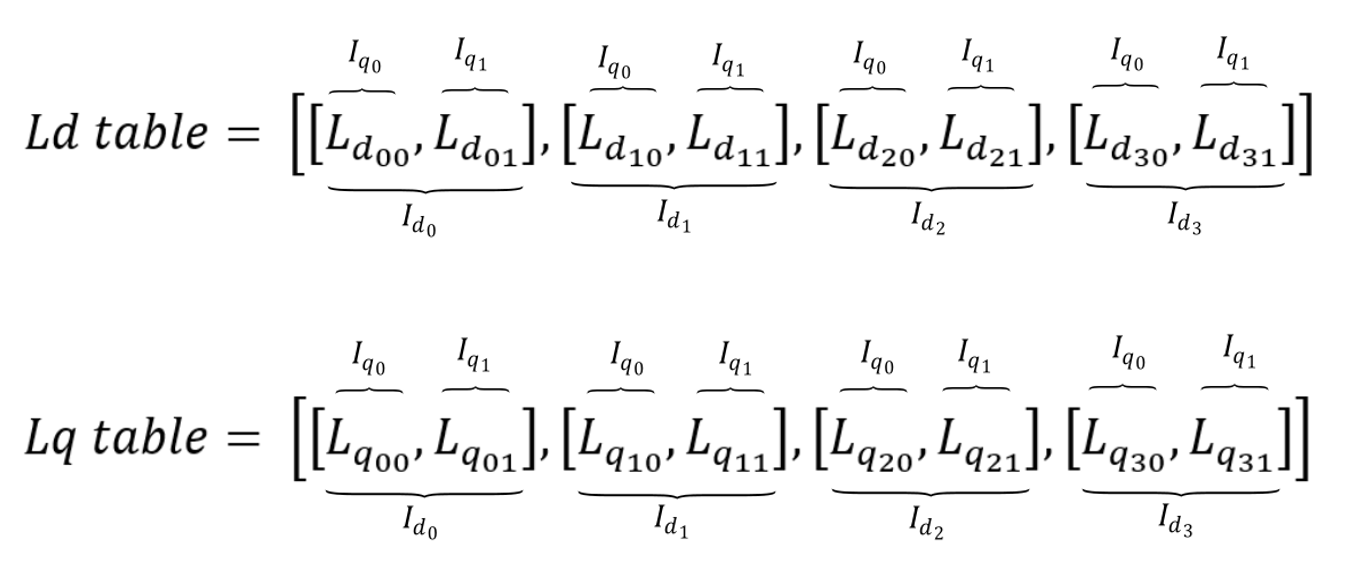
id_vector = [-40.0, -20.0, 0.0, 20.0, 40.0]
iq_vector = [-40.0, -20.0, 0.0, 20.0, 40.0]
Ld_table = [[0.00203118, 0.00188417, 0.00186383, 0.00188366, 0.00201026],
[0.00217976, 0.00297238, 0.00325188, 0.0029855, 0.00223459],
[0.00226518, 0.00283656, 0.00399657, 0.00280727, 0.00218666],
[0.0016353, 0.00171137, 0.00136793, 0.00178913, 0.00164534],
[0.00121342, 0.00096362, 0.000562082, 0.000967825, 0.00123179]]
Lq_table = [[0.00332706, 0.00419461, 0.0049565, 0.00419414, 0.00332745],
[0.00328404, 0.00520506, 0.00635444, 0.00520574, 0.00320567],
[0.00321572, 0.00538029, 0.00779154, 0.00535, 0.00319568],
[0.00293984, 0.00421955, 0.00547829, 0.00419697, 0.00290709],
[0.00273112, 0.00294274, 0.00323358, 0.00292902, 0.00271144]]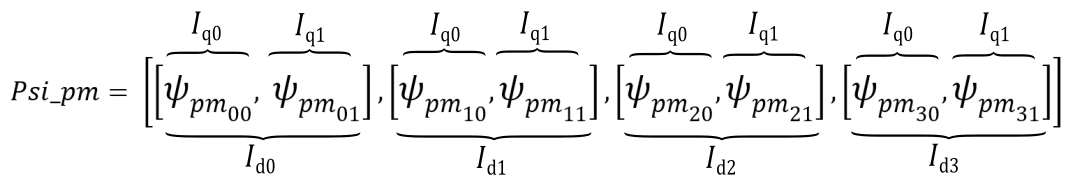
Psi_pm = [[0.0492472, 0.0433668, 0.0425532, 0.0433464, 0.0484104],
[0.0115952, 0.0274476, 0.0330376, 0.02771, 0.0126918],
[0.032, 0.032, 0.032, 0.032, 0.032],
[0.064706, 0.0662274, 0.0593586, 0.0677826, 0.0649068],
[0.0805368, 0.0705448, 0.05448328, 0.070713, 0.0812716]]
Besides the saturation, the permanent magnet synchronous machine model can include flux and torque spatial harmonics. The spatial effects are parametrized using lookup tables. Either the d- and q- axis current tables, or the d- and q- axis fluxes can be provided. In addition a torque table can be used if available.
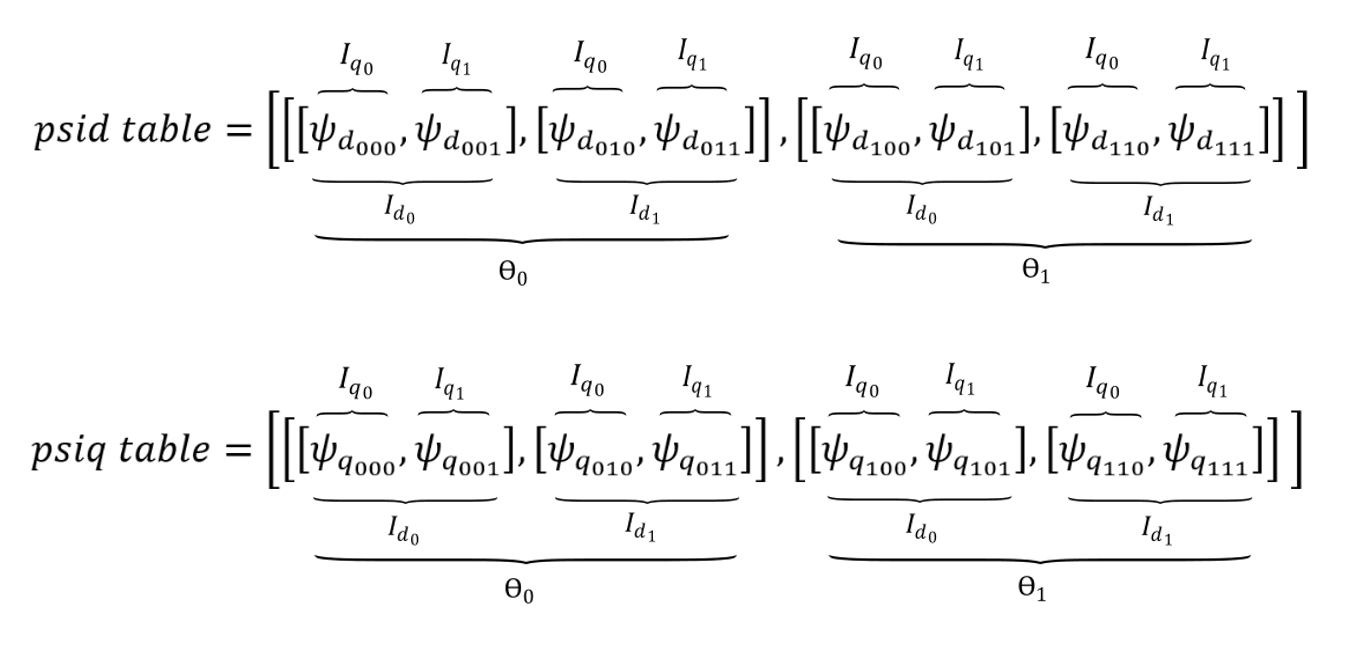
In case current tables are used, the corresponding mechanical angle vector and d- and q- axis flux vectors should be provided. Current tables should be provided in the form of nested Python lists, as shown in Figure 8.
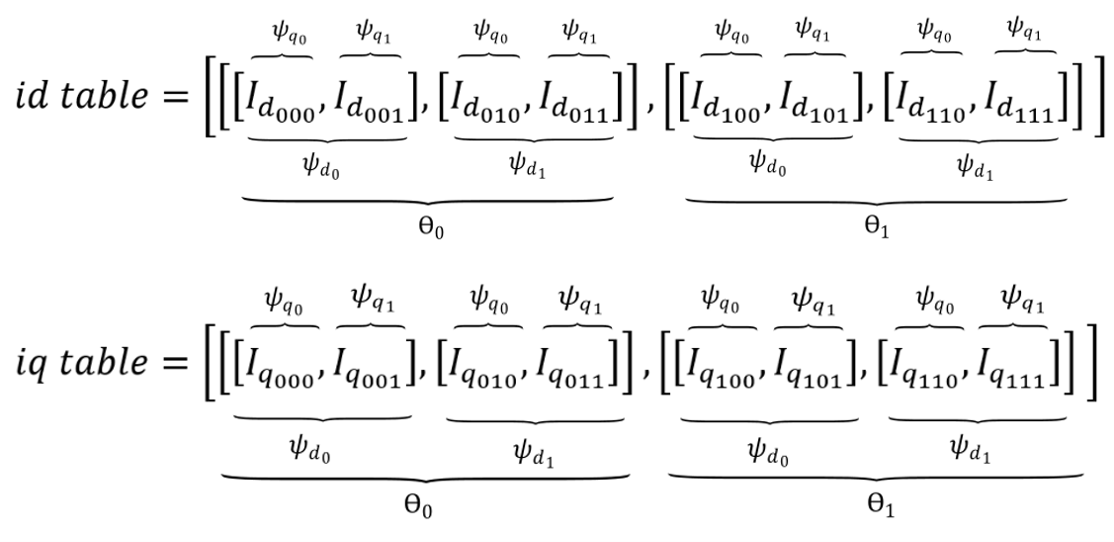
theta_vector = [0.0, 22.5, 45.0, 67.5, 90.0]
psid_vector = [-0.17759843289, -0.05223218269499999, 0.07313406750000001, 0.19850031769499998, 0.32386656789]
psiq_vector = [-0.32096138538, -0.16050672498000002, -5.2064580000010796e-05, 0.16040259582, 0.32085725622]
id_table = [[[-233.3333332266475, -257.7293103580557, -316.8917613233176, -333.57733038563356, -524.5012794984455],
[-214.1362540654731, -179.8644557067018, -175.6095994946196, -181.0505387996648, -215.40138388018036],
[-36.92650378240601, -69.0586289788347, -63.273581686244526, -70.17063151820344, -40.77023976035882],
[267.6898480190032, 52.86421935401373, 33.6580242832348, 51.462420971634344, 266.73575462947525],
[719.0939587350539, 504.29327242411, 327.8805498461348, 505.3208160059561, 739.8031312300301]],
[[-518.6412851693793, -311.47136454996325, -302.8497902237722, -323.26411347945736, -484.76183994292415],
[-252.47146382293585, -187.917041119209, -178.50886480262463, -187.11355282815586, -254.94255002472855],
[-27.470288415968216, -71.54367706056314, -68.17667941441388, -70.94691442014319, -21.575177136365266],
[263.634217105358, 49.99306039271444, 33.85662343644734, 50.02324023988559, 287.38372287122087],
[487.8066465303234, 475.34138513129415, 343.28954740870137, 481.09585672382536, 886.1748266387335]],
[[-1358.0867863490253, -294.7644181190118, -316.2886710922492, -333.2853796951674, -518.7741520618608],
[-221.40609547432894, -180.6126549799535, -175.32783498152025, -181.39213200802254, -219.73544940320306],
[-38.02088727721427, -69.39880536269256, -63.591831678615975, -70.03870613567662, -39.99592319412275],
[285.0269280215043, 52.55932476567479, 33.48729415990562, 51.772679745456095, 284.5939396855646],
[734.8557131136035, 496.92968546349186, 325.83589711204013, 497.4153052130295, 741.5352609429758]],
[[-481.31401210416425, -324.3217707320712, -303.1230653884171, -319.94141667622443, -522.4177238390196],
[-255.25215748840276, -187.61666345042423, -178.62561705508995, -187.38544556322825, -252.53421982058447],
[-21.136661228127362, -71.02227901516046, -68.21328231570936, -71.46227873128916, -28.007081413419538],
[287.9372590077436, 49.97715317296145, 33.84805488373838, 49.995135090980924, 263.72969918521676],
[889.7033083203972, 480.3358765356305, 343.4912680789687, 475.0335963743356, 480.71904954910747]],
[[-233.3333332266475, -257.7293103580557, -316.8917613233176, -333.57733038563356, -524.5012794984455],
[-214.1362540654731, -179.8644557067018, -175.6095994946196, -181.0505387996648, -215.40138388018036],
[-36.92650378240601, -69.0586289788347, -63.273581686244526, -70.17063151820344, -40.77023976035882],
[267.6898480190032, 52.86421935401373, 33.6580242832348, 51.462420971634344, 266.73575462947525],
[719.0939587350539, 504.29327242411, 327.8805498461348, 505.3208160059561, 739.8031312300301]]]
iq_table = [[[-505.7767327606924, -280.3879247672038, -0.004979635775945353, 81.56072354263337, 388.022701946017],
[-362.12146235920517, -65.11706948656484, -0.009006689778155635, 65.30288347665756, 360.9222744404181],
[-354.10565650294666, -56.28518525873091, -0.023007195469517627, 56.50559644760159, 354.42659138277475],
[-524.7129199636797, -63.51586774014338, -0.01907211767377474, 63.685563133071724, 523.6006117473538],
[-495.7745746168233, -223.462055435398, -0.043131396443353134, 223.51990260596656, 486.3133476657266]],
[[-385.5547021702862, -116.62652914866759, -2.4328564864150097, 91.1395141118797, 385.6202158255354],
[-348.5643372214161, -62.474866982627866, -1.6141778719715782, 63.915430122112376, 348.38827743061563],
[-344.2317951973277, -53.217841641598724, -0.2829134174492452, 53.444266829119286, 344.3158304893939],
[-559.9321686062336, -63.97847245191365, 0.007447138963719371, 63.605984497759785, 494.10502040433096],
[-744.2509414789488, -220.91783037329884, 5.646314291601746, 226.49417767658827, 426.45076352257263]],
[[-423.6191488886197, -197.28821469674918, -0.029109158152621717, 82.36933719822528, 396.7502646889574],
[-360.7616050698228, -65.10159040008985, -0.012464979197774825, 65.19745059787274, 359.1885431242987],
[-355.1172303301486, -56.04912760800942, -0.02066736464822022, 56.14819320909155, 354.974375905354],
[-501.7906358828526, -63.50620117139304, -0.018480103433047602, 63.56419813700306, 501.286806969245],
[-559.602743618543, -224.5269544340933, -0.040533278535931805, 224.41147249208652, 557.825916546207]],
[[-385.7921708213368, -91.33910828723663, 2.4258636983859017, 85.7541393098867, 384.9268913902443],
[-348.98598069158527, -64.04405447565786, 1.5924463454305111, 62.3542611407755, 347.9667145908271],
[-344.8627213215603, -53.50384725036235, 0.2523346366688757, 53.16092671197423, 343.8275503768093],
[-493.585223980637, -63.69991599380379, -0.039915498956818986, 63.89491923222919, 559.4722578117016],
[-424.3689382948914, -226.77181375007936, -5.718555609379146, 220.65695426867234, 749.2674814023829]],
[[-505.7767327606924, -280.3879247672038, -0.004979635775945353, 81.56072354263337, 388.022701946017],
[-362.12146235920517, -65.11706948656484, -0.009006689778155635, 65.30288347665756, 360.9222744404181],
[-354.10565650294666, -56.28518525873091, -0.023007195469517627, 56.50559644760159, 354.42659138277475],
[-524.7129199636797, -63.51586774014338, -0.01907211767377474, 63.685563133071724, 523.6006117473538],
[-495.7745746168233, -223.462055435398, -0.043131396443353134, 223.51990260596656, 486.3133476657266]]]Similarly, if flux tables are used, the corresponding mechanical angle vector and d- and q- axis current vectors should be provided. Flux tables should be provided in the form of nested Python lists, as shown in Figure 9.
theta_vector = [0.0, 22.5, 45.0, 67.5, 90.0]
id_vector = [-300.0, -150.0, 0.0, 150.0, 300.0]
iq_vector = [-300.0, -150.0, 0.0, 150.0, 300.0]
psid_table = [[[-0.092992778243, -0.13237251915, -0.16322147546, -0.13199157146, -0.10096193349],
[-0.0029494444998, -0.0083929999014, -0.029282905194, -0.0076414133404, -0.0013852031402],
[0.10440490171, 0.13644154255, 0.15471253507, 0.13778940842, 0.10531066716],
[0.18806823552, 0.22325538719, 0.2895834114, 0.22386412916, 0.18914953295],
[0.24210056956, 0.29284169573, 0.31930592972, 0.29305836422, 0.24223625458]],
[[-0.091400959733, -0.13475573804, -0.1749292499, -0.13344967473, -0.091505913051],
[0.010807087209, 0.0037682080669, -0.021177885886, 0.0050580803528, 0.013865421481],
[0.092979720949, 0.12680245185, 0.15720949383, 0.12830221086, 0.087157456451],
[0.18484038315, 0.23450690007, 0.28648263093, 0.23077487949, 0.1926615474],
[0.25554160821, 0.29268163818, 0.31651723863, 0.29290688656, 0.24704807003]],
[[-0.092992778243, -0.13237251915, -0.16322147546, -0.13199157146, -0.10096193349],
[-0.0029494444998, -0.0083929999014, -0.029282905194, -0.0076414133404, -0.0013852031402],
[0.10440490171, 0.13644154255, 0.15471253507, 0.13778940842, 0.10531066716],
[0.18806823552, 0.22325538719, 0.2895834114, 0.22386412916, 0.18914953295],
[0.24210056956, 0.29284169573, 0.31930592972, 0.29305836422, 0.24223625458]],
[[-0.091739531935, -0.13328209289, -0.17463672462, -0.13547915191, -0.091106283561],
[0.013974984528, 0.0048494387289, -0.021094593366, 0.0038619542714, 0.010457400808],
[0.086814220716, 0.12836592752, 0.15721463763, 0.1268579119, 0.093560402719],
[0.19321204329, 0.23077116549, 0.28644304894, 0.23461864289, 0.18407649916],
[0.24692274285, 0.29322474181, 0.31649361144, 0.29252690265, 0.25568574595]],
[[-0.092992778243, -0.13237251915, -0.16322147546, -0.13199157146, -0.10096193349],
[-0.0029494444998, -0.0083929999014, -0.029282905194, -0.0076414133404, -0.0013852031402],
[0.10440490171, 0.13644154255, 0.15471253507, 0.13778940842, 0.10531066716],
[0.18806823552, 0.22325538719, 0.2895834114, 0.22386412916, 0.18914953295],
[0.24210056956, 0.29284169573, 0.31930592972, 0.29305836422, 0.24223625458]]]
psiq_table = [[[-0.30267057235, -0.23873204132, -3.9742242698e-05, 0.23875633211, 0.30306175105],
[-0.31253878169, -0.27121809539, -2.2774634102e-05, 0.27112438205, 0.31253416609],
[-0.30684677005, -0.259210521, 6.9890032954e-05, 0.25852469615, 0.30648202774],
[-0.27257340534, -0.21876346148, -5.6740341132e-06, 0.21818529546, 0.27195331969],
[-0.24765650006, -0.14232824489, -6.7496759671e-07, 0.14203490233, 0.24758221016]],
[[-0.30314844055, -0.23689140972, 0.006975562102, 0.23574775985, 0.30351314397],
[-0.31581755327, -0.27606985039, 0.0039708418441, 0.27758097142, 0.31729056994],
[-0.31160085409, -0.26147296559, -4.8308402859e-06, 0.25981872322, 0.31166008436],
[-0.27067568901, -0.20688026038, -0.0023277204107, 0.21045636042, 0.2674130018],
[-0.23345074332, -0.14921595542, -0.0080053069921, 0.14892982912, 0.24254256344]],
[[-0.30267057235, -0.23873204132, -3.9742242698e-05, 0.23875633211, 0.30306175105],
[-0.31253878169, -0.27121809539, -2.2774634102e-05, 0.27112438205, 0.31253416609],
[-0.30684677005, -0.259210521, 6.9890032954e-05, 0.25852469615, 0.30648202774],
[-0.27257340534, -0.21876346148, -5.6740341132e-06, 0.21818529546, 0.27195331969],
[-0.24765650006, -0.14232824489, -6.7496759671e-07, 0.14203490233, 0.24758221016]],
[[-0.30347772145, -0.23574820553, -0.0070489207773, 0.23674928558, 0.30319387316],
[-0.31728064507, -0.27756643361, -0.003993128536, 0.27608560052, 0.31584615044],
[-0.31180110856, -0.25977013167, 2.3755038513e-05, 0.26144478567, 0.31137362134],
[-0.26710307569, -0.21045301205, 0.0023337513966, 0.2067830635, 0.27114401138],
[-0.24263545724, -0.14851609547, 0.0080074775793, 0.14941882074, 0.23337278011]],
[[-0.30267057235, -0.23873204132, -3.9742242698e-05, 0.23875633211, 0.30306175105],
[-0.31253878169, -0.27121809539, -2.2774634102e-05, 0.27112438205, 0.31253416609],
[-0.30684677005, -0.259210521, 6.9890032954e-05, 0.25852469615, 0.30648202774],
[-0.27257340534, -0.21876346148, -5.6740341132e-06, 0.21818529546, 0.27195331969],
[-0.24765650006, -0.14232824489, -6.7496759671e-07, 0.14203490233, 0.24758221016]]]
If a torque table is used, the corresponding mechanical angle vector and d- and q- axis current vectors should be provided. The torque table should be provided in the form of a nested Python list, as shown in Figure 10.
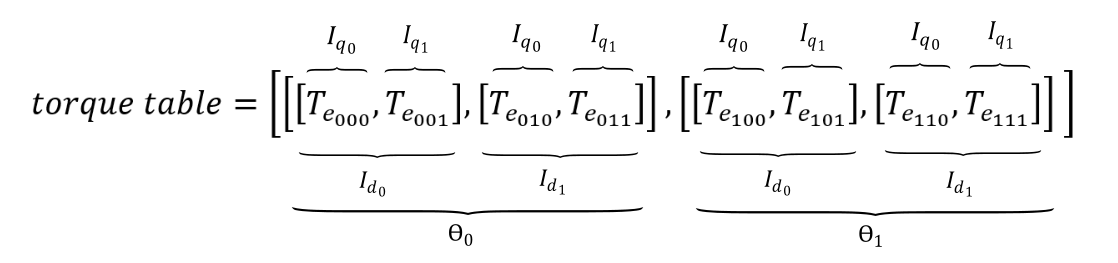
theta_vector_Te = [0.0, 22.5, 45.0, 67.5, 90.0]
id_vector_Te = [-300.0, -150.0, 0.0, 150.0, 300.0]
iq_vector_Te = [-300.0, -150.0, 0.0, 150.0, 300.0]
torque_table = [[[-461.04655919, -332.8598734071429, -1.1081461012, 332.19516658214286, 417.44568224],
[-310.17034254416666, -270.33688624595237, -0.6028780509916667, 269.57222287255956, 310.7964117258333],
[-181.42294254944443, -115.84374552687302, -0.13964706623777776, 116.38231039379764, 182.8068861733333],
[-71.39653398216667, -22.090781084223217, -0.2480898520933333, 22.702675578991077, 72.44508516358334],
[-17.389187999, 3.0152441219300004, -0.31449026734, -3.308692608017501, 17.560602092]],
[[-406.5500464167241, -330.2185009995751, -7.2103075736586435, 323.99610574970444, 393.13764143206896],
[-303.17428486106326, -258.37521056718805, -1.4688384703044242, 242.9134570621413, 279.117122536839],
[-193.58256053022032, -126.93593080655926, -0.04663152688847841, 115.51015942860606, 185.61982493497604],
[-82.87228742445406, -20.587316537185636, -2.0893218356421634, 18.94765146882643, 68.77152552149352],
[-11.835865058366366, 2.80535151599267, -4.42165218217588, -6.2915582802488705, 16.960317375474148]],
[[-434.3803288555173, -329.51918068817736, -0.978479661904311, 328.7406081689655, 411.19810940724136],
[-309.23001032433905, -266.99211121801216, -0.5271894872158025, 266.1513282419253, 308.8419751629023],
[-181.02066051524906, -115.72874560938229, -0.13495381758771985, 115.85456795407985, 181.61551272879308],
[-72.77033463190806, -21.76985714980434, -0.2098273789515268, 21.9973558092166, 73.07922227660056],
[-16.708790785637927, 4.057159049915403, -0.23920637331069816, -4.498794611058943, 16.951112875275868]],
[[-395.9036097492242, -327.4350358606774, 4.104308753119819, 326.5365435651355, 404.0223042287069],
[-281.1730763519828, -244.62356556263495, 0.18221397225358488, 256.6490751091097, 300.84784955936783],
[-186.29659264766764, -116.5868949390978, -0.24199789123452298, 126.11889945284456, 193.75063811867813],
[-70.16874964458478, -19.41093047180019, 1.6817520097219076, 20.172507135146788, 81.2285505420783],
[-16.95140339243965, 5.482216391687682, 3.8769159026112012, -3.4494739236762335, 12.050726226853453]],
[[-461.04655919, -332.8598734071429, -1.1081461012, 332.19516658214286, 417.44568224],
[-310.17034254416666, -270.33688624595237, -0.6028780509916667, 269.57222287255956, 310.7964117258333],
[-181.42294254944443, -115.84374552687302, -0.13964706623777776, 116.38231039379764, 182.8068861733333],
[-71.39653398216667, -22.090781084223217, -0.2480898520933333, 22.702675578991077, 72.44508516358334],
[-17.389187999, 3.0152441219300004, -0.31449026734, -3.308692608017501, 17.560602092]]]
In all cases the mechanical angle vector must be given as a list ranging from 0 to 360/pole_pairs. The number of points available for all lookup tables used is 215. If the total number of points provided in the lookup tables exceeds this number, the tables will be rescaled to work with fewer points. The resulting tables may have lower resolution than the original ones.
Iron Losses
If iron losses are included, the corresponding direct and quadrature axis iron loss currents are calculated as follows:
Direct and quadrature axis components of iron loss currents are added to the corresponding components of stator currents, which provide the machine's electromagnetic torque:
| symbol | description |
|---|---|
| ψds | Direct axis component of the stator flux [Wb] |
| ψqs | Quadrature axis component of the stator flux [Wb] |
| vds | Direct axis component of the stator voltage [V] |
| vqs | Quadrature axis component of the stator voltage [V] |
| ids | Direct axis component of the stator current [A] |
| iqs | Quadrature axis component of the stator current [A] |
| id,Fe | Direct axis component of the iron loss current [A] |
| iq,Fe | Quadrature axis component of the iron loss current [A] |
| idm | Direct axis component of the stator current which determines torque production [A] |
| iqm | Quadrature axis component of the stator current which determines torque production [A] |
| RFe | Iron loss resistance [Ω] |
| PFe | Total iron losses [W] |
| ωr | Rotor electrical speed [rad/s] ( ) |
An example of a PMSM model including iron losses can be found in the pmsm iron losses.tse example in our Examples Explorer [examples\models\electrical drives\pmsm iron losses].
Ports
- A (electrical)
- Stator winding phase A port.
- B (electrical)
- Stator winding phase B port.
- C (electrical)
- Stator winding phase C port.
- in
- Available if Model Load source is selected or Dynamic flux is enabled (Dynamic flux is available only if Model type is set to linear)
- Input vector description and order:
- in[0] = model_load - if Model Load source is selected and Dynamic flux is enabled/disabled
- in[0] = Permanent magnet's flux [Wb] - if SCADA / external Load source is selected and Dynamic flux is enabled
- in[1] = Permanent magnet's flux [Wb] - if Model Load source is selected and Dynamic flux is enabled
- PFe
- Iron losses input port
- Available only if Iron losses are enabled (Iron losses is available only if Model type is set to nonlinear - spatial harmonics)
Iron losses feature is not supported in TyphoonSim yet.
Electrical (Tab)
- Model Type
- Specifies machine model implementation.
- Several levels of model fidelity are available - linear, nonlinear, or nonlinear - spatial harmonics.
- Saturation
- Available if Model Type is set to nonlinear.
- Following saturation types can be specified - flux vs current, absolute inductance vs current, or incremental inductance vs current.
- Maps
- Available if Model Type is set to nonlinear - spatial harmonics.
- Following saturation types can be specified - flux vs currents, theta or current vs fluxes, theta.
- Rs
- Stator phase resistance [Ω]
- Ld
- Available if Model Type is set to linear.
- Direct axis inductance [H]
- Lq
- Available if Model Type is set to linear.
- Quadrature axis inductance [H]
- Psi_pm
- Available if Model Type is set to linear, nonlinear - absolute inductance vs current, nonlinear - incremental inductance vs current.
- Flux amplitude established in stator phases by rotor permanent magnets [Wb]
- If Model Type is set to nonlinear - absolute inductance vs current or nonlinear - incremental inductance vs current, flux can be either a scalar value or current dependent. If Model Type is set to linear, flux has to be a scalar value.
- Dynamic flux
- This property is only available if the selected Model Type is linear.
- Enables external control of the amplitude of the permanent magnet's flux linkage in the stator phase winding during simulation runtime.
- When enabled, a machine input terminal is either created or extended by a new input for defining this flux value in Wb. More information can be found in the dedicated ports section.
- id vector
- Available if Model Type is set to nonlinear or nonlinear - spatial harmonics - flux vs currents, theta.
- List of stator current direct axis component values [A]
- iq vector
- Available if Model Type is set to nonlinear or nonlinear - spatial harmonics - flux vs currents, theta.
- List of stator current quadrature axis component values [A]
- theta vector
- Available if Model Type is set to nonlinear - spatial harmonics.
- List of mechanical angle values [⁰]
- psid vector
- Available if Model Type is set to nonlinear - spatial harmonics - current vs fluxes, theta.
- List of stator flux direct axis component values [Wb]
- psiq vector
- Available if Model Type is set to nonlinear - spatial harmonics - current vs fluxes, theta.
- List of stator flux quadrature axis component values [Wb]
- id table
- Available if Model Type is set to nonlinear - spatial harmonics - current vs fluxes, theta.
- Table of stator current direct axis component values [A]
- iq table
- Available if Model Type is set to nonlinear - spatial harmonics - current vs fluxes, theta.
- Table of stator current quadrature axis component values [A]
- psid table
- Available if Model Type is set to nonlinear - flux vs currents, or nonlinear - spatial harmonics - flux vs currents, theta.
- Table of stator flux direct axis component values [Wb]
- psiq table
- Available if Model Type is set to nonlinear - flux vs currents, or nonlinear - spatial harmonics - flux vs currents, theta.
- Table of stator flux quadrature axis component values [Wb]
- Ld table
- Available if Model Type is set to nonlinear - absolute inductance vs current, or nonlinear - incremental inductance vs current.
- Table of stator inductance direct axis component values [H]
- Lq table
- Available if Model Type is set to nonlinear - absolute inductance vs current, or nonlinear - incremental inductance vs current.
- Table of stator inductance quadrature axis component values [H]
- Use torque table
- Available if Model Type is set to nonlinear - spatial harmonics.
- When enabled, the electrical torque will be calculated using a Look-up table.
- theta vector Te
- Available if Use torque table is enabled.
- List of mechanical angle values used as input to the torque lookup table [⁰]
- id vector Te
- Available if Use torque table is enabled.
- List of stator current direct axis component values used as input to the torque lookup table [A]
- iq vector Te
- Available if Use torque table is enabled.
- List of stator current quadrature axis component values used as input to the torque lookup table [A]
- torque table
- Available if Use torque table is enabled.
- Table of torque values [Nm]
- Iron losses
Iron losses feature is not supported in TyphoonSim yet.
- In real-time/VHIL simulation, this property is only available if the selected Model Type is nonlinear - spatial harmonics.
- If iron losses are included, the corresponding direct and quadrature axis iron loss currents are calculated.
- When enabled, additional machine input terminal is created.
- More information can be found in the dedicated Iron Losses section.
Mechanical (Tab)
- pms
- Machine number of pole pairs
-
Star/delta
- Stator winding connection (star or delta)
- Jm
- Combined rotor and load moment of inertia [kgm2]
- Friction coefficient
- Machine viscous friction coefficient [Nms]
- Unconstrained mechanical angle
- Limiting mechanical angle between 0 and 2π
Load (Tab)
- Load source
- Load source can be set from SCADA/external or from model (in model case, one signal processing input will appear).
- In TyphoonSim, if SCADA/external is chosen as Load source, analog signals are read from the internal virtual IO bus. Hence, if some signal is sent to analog ouput 1, it will appear on analog input 1.
- External/Model load type
- Load type: torque or speed
- Load ai pin
- Load ai pin for external torque/speed command.
- In real-time/VHIL simulation, Load ai pin represent HIL analog input address for external torque command.
- In TyphoonSim, analog signals are read from the internal virtual IO bus. Hence, if some signal is sent to analog ouput 1, it will appear on analog input 1.
- Available only if SCADA/external is set as Load source.
- Load ai offset
- Assigned offset value to the input signal representing external torque command.
- Available only if SCADA/external is set as Load source.
- Load ai gain
- Assigned gain value to the input signal representing external torque command.
- Available only if SCADA/external is set as Load source.
External load enables you to use an analog input signal from a HIL/TyphoonSim (internal virtual IO bus in TyphoonSim) analog channel with the load_ai_pin address as an external torque/speed load, and to assign offset (V) and gain (Nm/V) to the input signal, according to the formula:
Feedback (Tab)
- Encoder ppr
- Incremental encoder number of pulses per revolution
- Encoder Z pulse length
- Z digital signal pulse length in periods. Can be Quarter length or Full period (default)
- Resolver pole pairs
- Resolver number of pole pairs
- Resolver carrier source
- Resolver carrier signal source selection (internal or external)
- Resolver carrier frequency
- Resolver carrier signal frequency (internal carrier) [Hz]
- Available only if the Resolver carrier source property is set to internal
- External resolver carrier source type
- External resolver carrier signal source type selection (single ended or differential)
- Available only if the Resolver carrier source property is set to external
- Resolver ai pin 1
- Resolver carrier input channel 1 address (external carrier)
- Available only if the Resolver carrier source property is set to external
- In TyphoonSim, analog signals are read from the internal virtual IO bus. Hence, if some signal is sent to analog ouput 1, it will appear on analog input 1.
- Resolver ai pin 2
- Resolver carrier input channel 2 address (external carrier)
- Available only if the Resolver carrier source property is set to externaland External resolver carrier source type property is set to differential
- In TyphoonSim, analog signals are read from the internal virtual IO bus. Hence, if some signal is sent to analog ouput 1, it will appear on analog input 1.
- Resolver ai offset
- Resolver carrier input channel offset (external carrier)
- Available only if the Resolver carrier source property is set to external
- In TyphoonSim, analog signals are read from the internal virtual IO bus. Hence, if some signal is sent to analog ouput 1, it will appear on analog input 1.
- Resolver ai gain
- Resolver carrier input channel gain (external carrier)
- Available only if the Resolver carrier source property is set to external
- In TyphoonSim, analog signals are read from the internal virtual IO bus. Hence, if some signal is sent to analog ouput 1, it will appear on analog input 1.
- Absolute encoder protocol
- Standardized protocol providing the absolute machine encoder position.
Absolute encoder protocol is ignored in TyphoonSim. Changing its value will not affect TyphoonSim simulation at all.
- Singleturn bits
- Number of machine absolute encoder singleturn bits.
- Available only if Absolute encoder protocol is not None.
Absolute encoder protocol is ignored in TyphoonSim. Changing its value will not affect TyphoonSim simulation at all.
- Enable multiturn
- Enables multiturn absolute encoder support.
- Available only if Absolute encoder protocol is not None.
Absolute encoder protocol is ignored in TyphoonSim. Changing its value will not affect TyphoonSim simulation at all.
- Multiturn bits
- Number of machine absolute encoder multiturn bits.
- Available only if Enable multiturn is checked.
Absolute encoder protocol is ignored in TyphoonSim. Changing its value will not affect TyphoonSim simulation at all.
- EnDat/SSI/BiSS clock DI pin
- Clock digital input pin for the chosen absolute encoder protocol type.
- Available only if Absolute encoder protocol is not None.
Absolute encoder protocol is ignored in TyphoonSim. Changing its value will not affect TyphoonSim simulation at all.
- Clock DI logic
- Clock DI pin logic: active high/active low.
- Available only if Absolute encoder protocol is not None.
Absolute encoder protocol is ignored in TyphoonSim. Changing its value will not affect TyphoonSim simulation at all.
- EnDat data DI pin
- EnDat data digital input pin.
- Available only if Absolute encoder protocol is EnDat.
Absolute encoder protocol is ignored in TyphoonSim. Changing its value will not affect TyphoonSim simulation at all.
- Data DI logic
- EnDat data DI pin logic: active high/active low.
- Available only if Absolute encoder protocol is EnDat.
Absolute encoder protocol is ignored in TyphoonSim. Changing its value will not affect TyphoonSim simulation at all.
If an external resolver carrier source is selected, the source signal type can be set as either single ended or differential. The single ended external resolver carrier source type enables use of an analog input signal from the HIL/TyphoonSim (internal virtual IO bus in TyphoonSim) analog channel with the res_ai_pin_1 address as the external carrier source. Additionally, offset (V) and gain (V/V) values can be assigned to the input signal, according to the formula:
The differential external resolver carrier source type enables use of two analog input signals from the HIL/TyphoonSim (internal virtual IO bus in TyphoonSim) analog channels with the res_ai_pin_1 and the res_ai_pin_2 addresses. Analog signals from these HIL/TyphoonSim (internal virtual IO bus in TyphoonSim) analog inputs are subtracted, and the resulting signal is used as the external differential carrier source. Additionally, offset (V) and gain (V/V) values can be assigned to the input signal (similarly to the single ended case), according to the formula:
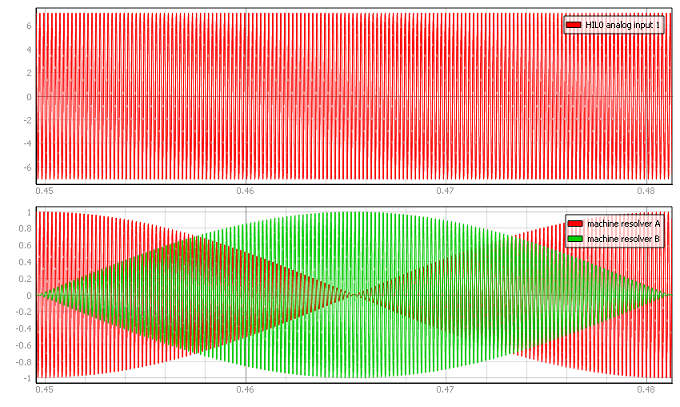
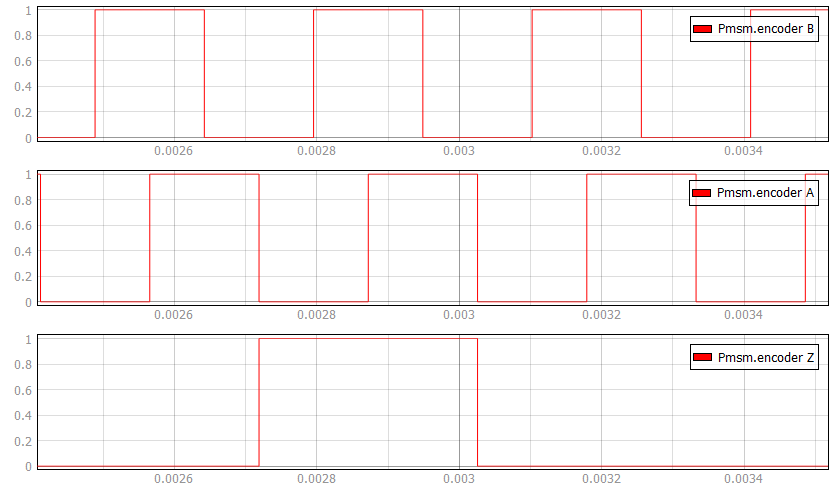
The following expression must hold in order to properly generate the encoder signals:
| symbol | description |
|---|---|
| enc_ppr | Encoder number of pulses per revolution |
| fm | Rotor mechanical frequency [Hz] |
| Ts | Simulation time step [s] |
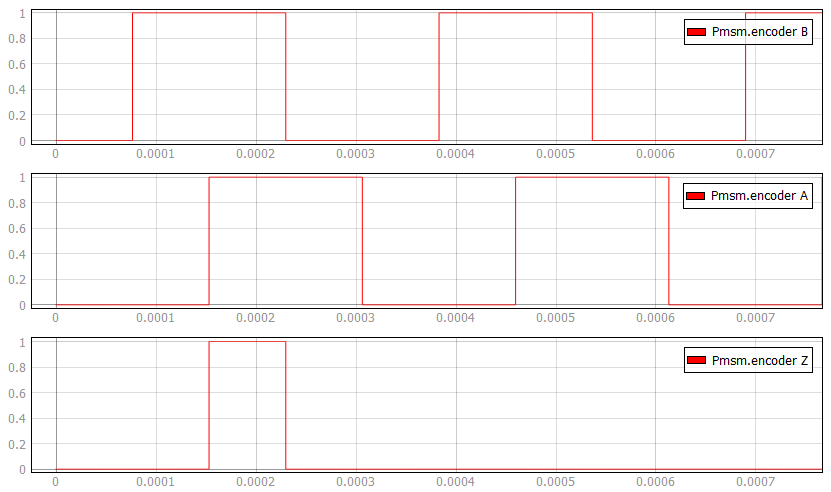
Advanced (Tab)
- Theta_ab
- Position of the stationary αβ reference frame, in respect to the stator phase a axis [rad]
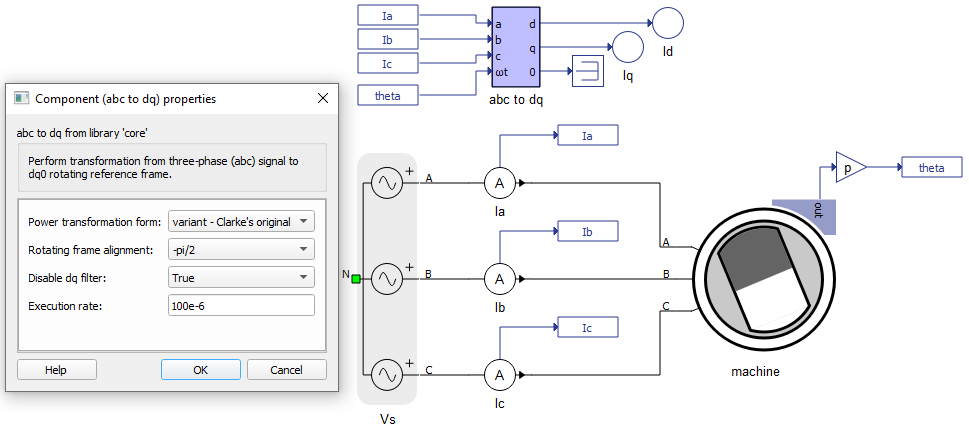
The machine model output variables (currents, voltages and fluxes) can be observed from a stationary reference frame. There are two widely used approaches in electrical machine modeling: in the first, the alpha axis of the stationary reference frame lags by 90 degrees in regard to the stator phase a axis (used by default, and indicated in a of Figure 14). In the second one, the alpha axis is aligned with the stator phase a axis (indicated in b of Figure 14). Setting the Theta_ab property allows for selecting between these two situations.
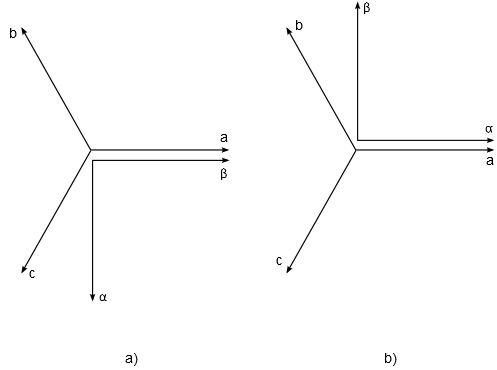
It is important to know the value of Theta_ab when the rotor position feedback is necessary. As an example, if a model uses the mechanical angle as a feedback signal and feeds it to one of the ABC to DQ, Alpha Beta to DQ, DQ to ABC or DQ to Alpha Beta transformation blocks, the same transformation angle offset value should be used in both components to ensure the expected simulation results.
Snubber (Tab)
- Rsnb stator
- Stator snubber resistance value [Ω]
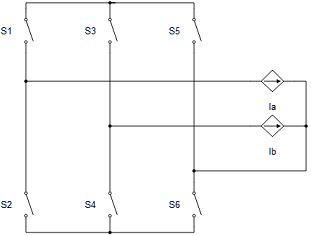
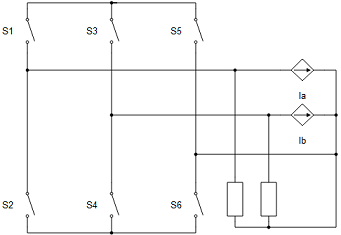
All machines with current source based circuit interfaces have the Snubber tab in the properties window where the value of snubber resistance can be set. Snubbers are necessary in the cases when an inverter or a contactor is directly connected to the machine terminals. This value can be set to infinite (inf), but it is not recommended when a machine is directly connected to the inverter since there will be a current source directly connected to an open switch. In this case, one of each switch pairs S1 and S2, S3 and S4, and S5 and S6 will be forced closed by the circuit solver in order to avoid the topological conflicts. On the other hand, with finite snubber values, there's always a path for the currents Ia and Ib, so all inverter switches can be open in this case. Circuit representations of this circuit without and with snubber resistors are shown in Figure 16 and Figure 17 respectively. Snubbers are connected across the current sources.
Output (Tab)
This block tab enables a single, vectorized signal output from the machine. The output vector contains selected machine mechanical and/or electrical variables in the same order as listed in this tab.
- Execution rate
- Signal processing output execution rate [s]
- Electrical torque
- Machine electrical torque [Nm]
- Mechanical speed
- Machine mechanical angular speed [rad/s]
- Mechanical angle
- Machine mechanical angle [rad]
- Stator alpha axis current
- Alpha axis component of the stator current [A]
- Stator beta axis current
- Beta axis component of the stator current [A]
- Stator d-axis current
- Direct axis component of the stator current [A]
- Stator q-axis current
- Quadrature axis component of the stator current [A]
- Stator alpha axis flux
- Alpha axis component of the stator flux [Wb]
- Stator beta axis flux
- Beta axis component of the stator flux [Wb]
- Stator d-axis flux
- Direct axis component of the stator flux [Wb]
- Stator q-axis flux
- Quadrature axis component of the stator flux [Wb]
Extras (Tab)
The Extras tab gives you the opportunity to set Signal Access Management for the component.
- Public - Components marked as public expose their signals on all levels.
- Protected - Components marked as protected will hide their signals to components outside of their first locked parent component.
- Inherit - Components marked as inherit will take the nearest parent 'signal_access' property value that is set to a value other than inherit.