Six Phase Wound Rotor Synchronous Machine (Double Stator)
Description of the Six Phase Wound Rotor Synchronous Machine (Double Stator) component in Schematic Editor.
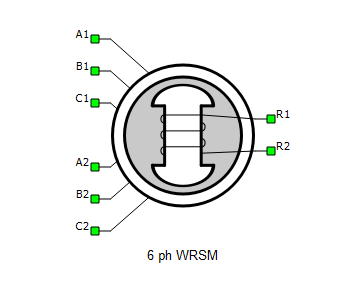
A1, B1, and C1 are the stator winding 1 terminals. A2, B2, and C2 are the stator winding 2 terminals. Stator windings use the current source interface. R1 and R2 are the field winding terminals. Both damper windings on the rotor are short-circuited and without output terminals. The rotor winding uses the single phase variant of the current source interface.
Electrical sub-system model
The electrical part of the machine is represented by the following system of equations, modeled in the rotating dq reference frame. The dq reference frame is attached to the rotor, and the direct axis is aligned with the field winding axis.
All rotor variables and parameters are referred to the stator with an appropriate turns ratio. To illustrate this, if you apply voltage vfdr at the field winding terminals, it is transformed to the stator value vfd with the following equation:
Similarly, the calculated rotor currents (field winding current ifd and damper winding currents ikd and ikq) are referred back to the real rotor windings values ifdr, ikdr, and ikqr, through the following equations:
| symbol | description |
|---|---|
| ψds1 | Direct axis component of the stator winding 1 flux [Wb] |
| ψqs1 | Quadrature axis component of the stator winding 1 flux [Wb] |
| ψds2 | Direct axis component of the stator winding 2 flux [Wb] |
| ψqs2 | Quadrature axis component of the stator winding 2 flux [Wb] |
| ψkd | Direct axis component of the damper winding flux, referred to the stator [Wb] |
| ψkq | Quadrature axis component of the damper winding flux, referred to the stator [Wb] |
| ψfd | Field winding flux, referred to the stator [Wb] |
| ids1 | Direct axis component of the stator winding 1 current [A] |
| iqs1 | Quadrature axis component of the stator winding 1 current [A] |
| ids2 | Direct axis component of the stator winding 2 current [A] |
| iqs2 | Quadrature axis component of the stator winding 2 current [A] |
| ikd | Direct axis component of the damper winding current, referred to the stator [A] |
| ikdr | Direct axis component of the damper winding current [A] |
| ikq | Quadrature axis component of the damper winding current, referred to the stator [A] |
| ikqr | Quadrature axis component of the damper winding current [A] |
| ifd | Field winding current, referred to the stator [A] |
| ifdr | Field winding current [A] |
| vds1 | Direct axis component of the stator winding 1 voltage [V] |
| vqs1 | Quadrature axis component of the stator winding 1 voltage [V] |
| vds2 | Direct axis component of the stator winding 2 voltage [V] |
| vqs2 | Quadrature axis component of the stator winding 2 voltage [V] |
| vfd | Field winding voltage, referred to the stator [V] |
| vfdr | Field winding voltage [V] |
| vkd | Direct axis component of the damper winding voltage, referred to the stator [V] |
| vkq | Quadrature axis component of the damper winding voltage, referred to the stator [V] |
| Rs1 | Stator winding 1 phase resistance [Ω] |
| Rs2 | Stator winding 2 phase resistance [Ω] |
| Rkd | Direct axis damper winding resistance, referred to the stator [Ω] |
| Rkq | Quadrature axis damper winding resistance, referred to the stator [Ω] |
| Rfd | Field winding resistance, referred to the stator [Ω] |
| Lls1 | Stator winding 1 phase leakage inductance [H] |
| Lls2 | Stator winding 2 phase leakage inductance [H] |
| Lls12 | Common leakage inductance of stator windings 1 and 2 [H] |
| Lmd | Direct axis magnetizing (mutual, main) inductance [H] |
| Lmq | Quadrature axis magnetizing (mutual, main) inductance [H] |
| Llkd | Direct axis damper winding leakage inductance, referred to the stator [H] |
| Llkq | Quadrature axis damper winding leakage inductance, referred to the stator [H] |
| Llfd | Direct axis field winding leakage inductance, referred to the stator [H] |
| ωr | Rotor electrical speed [rad/s] ( ) |
| p | Machine number of pole pairs |
| Te | Machine developed electromagnetic torque [Nm] |
Mechanical sub-system model
Motion equation:
| Symbol | Description |
|---|---|
| ωm | Rotor mechanical speed [rad/s] |
| Jm | Combined rotor and load moment of inertia [kgm2] |
| Te | Machine developed electromagnetic torque [Nm] |
| Tl | Shaft mechanical load torque [Nm] |
| b | Machine viscous friction coefficient [Nms] |
| θm | Rotor mechanical angle [rad] |
Ports
- A1 (electrical)
- Stator winding 1 phase A port.
- B1 (electrical)
- Stator winding 1 phase B port.
- C1 (electrical)
- Stator winding 1 phase C port.
- A2 (electrical)
- Stator winding 2 phase A port.
- B2 (electrical)
- Stator winding 2 phase B port.
- C2 (electrical)
- Stator winding 2 phase C port.
- R1 (electrical)
- Field winding port 1.
- R2 (electrical)
- Field winding port 2.
- in
- Available if Model Load source is selected.
Electrical (Tab)
- Rs1
- Stator winding 1 phase resistance [Ω]
- Lls1
- Stator winding 1 phase leakage inductance [H]
- Rs2
- Stator winding 2 phase resistance [Ω]
- Lls2
- Stator winding 2 phase leakage inductance [H]
- Lls12
- Common leakage inductance of stator windings 1 and 2 [H]
- Lmd
- Direct axis magnetizing (mutual, main) inductance [H]
- Lmq
- Quadrature axis magnetizing (mutual, main) inductance [H]
- Rf
- Field winding resistance, referred to the stator [Ω]
- Llfd
- Direct axis field winding leakage inductance, referred to the stator [H]
-
Rkd
- Direct axis damper winding resistance, referred to the stator [Ω]
- Rkq
- Quadrature axis damper winding resistance, referred to the stator [Ω]
- Llkd
- Direct axis damper winding leakage inductance, referred to the stator [H]
-
Llkq
- Quadrature axis damper winding leakage inductance, referred to the stator [H]
- Ns/Nfd
- Turns ratio between the stator phase winding and the field winding used for transforming field winding variables to the stator-side
-
Ns/Nkd
- Turns ratio between the stator phase winding and the direct axis damper winding used for transforming damper winding variables to the stator-side
Ns/Nkd turns ratio is not supported in TyphoonSim. Changing its value will not affect TyphoonSim simulation at all.
- Ns/Nkq
- Turns ratio between the stator phase winding and the quadrature axis damper winding used for transforming damper winding variables to the stator-side
Ns/Nkq turns ratio is not supported in TyphoonSim. Changing its value will not affect TyphoonSim simulation at all.
Mechanical (Tab)
- pms
- Machine number of pole pairs
- Star/delta w1
- Stator winding 1 connection (star or delta)
- Star/delta w2
- Stator winding 2 connection (star or delta)
- Jm
- Combined rotor and load moment of inertia [kgm2]
- Friction coefficient
- Machine viscous friction coefficient [Nms]
- Unconstrained mechanical angle
- Limiting mechanical angle between 0 and 2π
Load (Tab)
- Load source
- Load source can be set from SCADA/external or from model (in model case, one signal processing input will appear).
- In TyphoonSim, if SCADA/external is chosen as Load source, analog signals are read from the internal virtual IO bus. Hence, if some signal is sent to analog ouput 1, it will appear on analog input 1.
- External/Model load type
- Load type: torque or speed
- Load ai pin
- Load ai pin for external torque/speed command.
- In real-time/VHIL simulation, Load ai pin represent HIL analog input address for external torque command.
- In TyphoonSim, analog signals are read from the internal virtual IO bus. Hence, if some signal is sent to analog ouput 1, it will appear on analog input 1.
- Available only if SCADA/external is set as Load source.
- Load ai offset
- Assigned offset value to the input signal representing external torque command.
- Available only if SCADA/external is set as Load source.
- Load ai gain
- Assigned gain value to the input signal representing external torque command.
- Available only if SCADA/external is set as Load source.
External load enables you to use an analog input signal from a HIL/TyphoonSim (internal virtual IO bus in TyphoonSim) analog channel with the load_ai_pin address as an external torque/speed load, and to assign offset (V) and gain (Nm/V) to the input signal, according to the formula:
Feedback (Tab)
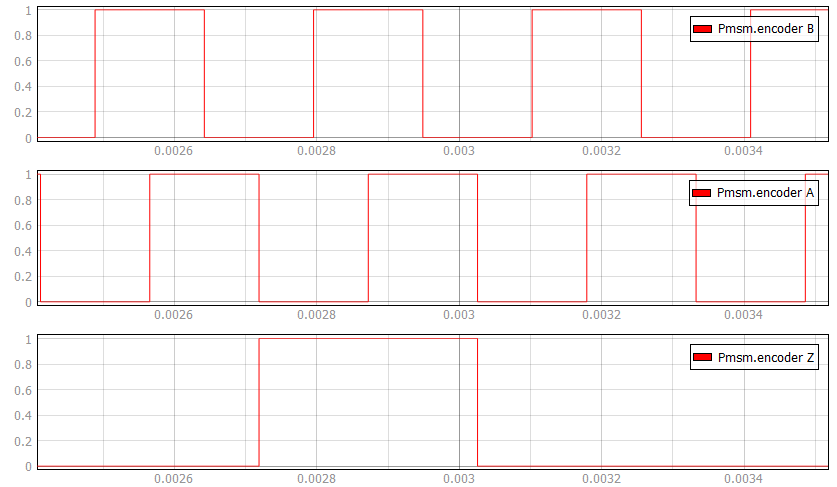
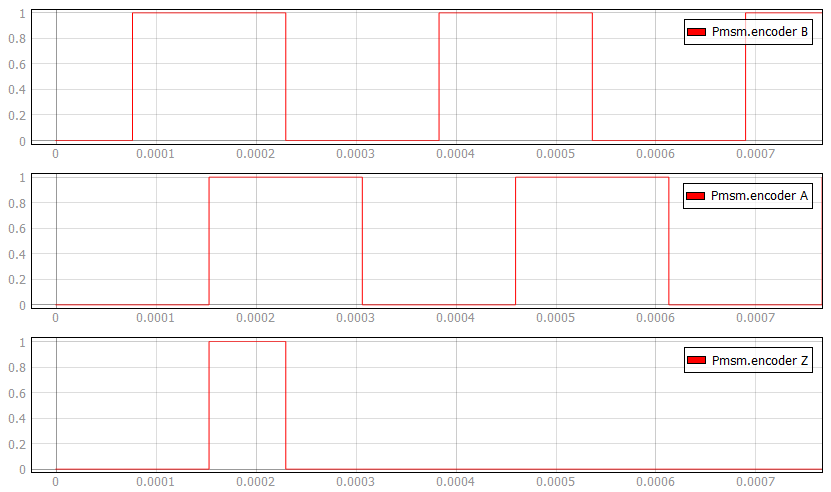
- Encoder ppr
- Incremental encoder number of pulses per revolution
- Encoder Z pulse length
- Z digital signal pulse length in periods. Can be Quarter length or Full period (default)
- Resolver pole pairs
- Resolver number of pole pairs
- Resolver carrier source
- Resolver carrier signal source selection (internal or external)
- Resolver carrier frequency
- Resolver carrier signal frequency (internal carrier) [Hz]
- Available only if the Resolver carrier source property is set to internal
- External resolver carrier source type
- External resolver carrier signal source type selection (single ended or differential)
- Available only if the Resolver carrier source property is set to external
- Resolver ai pin 1
- Resolver carrier input channel 1 address (external carrier)
- Available only if the Resolver carrier source property is set to external
- In TyphoonSim, analog signals are read from the internal virtual IO bus. Hence, if some signal is sent to analog ouput 1, it will appear on analog input 1.
- Resolver ai pin 2
- Resolver carrier input channel 2 address (external carrier)
- Available only if the Resolver carrier source property is set to externaland External resolver carrier source type property is set to differential
- In TyphoonSim, analog signals are read from the internal virtual IO bus. Hence, if some signal is sent to analog ouput 1, it will appear on analog input 1.
- Resolver ai offset
- Resolver carrier input channel offset (external carrier)
- Available only if the Resolver carrier source property is set to external
- In TyphoonSim, analog signals are read from the internal virtual IO bus. Hence, if some signal is sent to analog ouput 1, it will appear on analog input 1.
- Resolver ai gain
- Resolver carrier input channel gain (external carrier)
- Available only if the Resolver carrier source property is set to external
- In TyphoonSim, analog signals are read from the internal virtual IO bus. Hence, if some signal is sent to analog ouput 1, it will appear on analog input 1.
- Absolute encoder protocol
- Standardized protocol providing the absolute machine encoder position.
Absolute encoder protocol is ignored in TyphoonSim. Changing its value will not affect TyphoonSim simulation at all.
- Singleturn bits
- Number of machine absolute encoder singleturn bits.
- Available only if Absolute encoder protocol is not None.
Absolute encoder protocol is ignored in TyphoonSim. Changing its value will not affect TyphoonSim simulation at all.
- Enable multiturn
- Enables multiturn absolute encoder support.
- Available only if Absolute encoder protocol is not None.
Absolute encoder protocol is ignored in TyphoonSim. Changing its value will not affect TyphoonSim simulation at all.
- Multiturn bits
- Number of machine absolute encoder multiturn bits.
- Available only if Enable multiturn is checked.
Absolute encoder protocol is ignored in TyphoonSim. Changing its value will not affect TyphoonSim simulation at all.
- EnDat/SSI/BiSS clock DI pin
- Clock digital input pin for the chosen absolute encoder protocol type.
- Available only if Absolute encoder protocol is not None.
Absolute encoder protocol is ignored in TyphoonSim. Changing its value will not affect TyphoonSim simulation at all.
- Clock DI logic
- Clock DI pin logic: active high/active low.
- Available only if Absolute encoder protocol is not None.
Absolute encoder protocol is ignored in TyphoonSim. Changing its value will not affect TyphoonSim simulation at all.
- EnDat data DI pin
- EnDat data digital input pin.
- Available only if Absolute encoder protocol is EnDat.
Absolute encoder protocol is ignored in TyphoonSim. Changing its value will not affect TyphoonSim simulation at all.
- Data DI logic
- EnDat data DI pin logic: active high/active low.
- Available only if Absolute encoder protocol is EnDat.
Absolute encoder protocol is ignored in TyphoonSim. Changing its value will not affect TyphoonSim simulation at all.
If an external resolver carrier source is selected, the source signal type can be set as either single ended or differential. The single ended external resolver carrier source type enables use of an analog input signal from the HIL/TyphoonSim (internal virtual IO bus in TyphoonSim) analog channel with the res_ai_pin_1 address as the external carrier source. Additionally, offset (V) and gain (V/V) values can be assigned to the input signal, according to the formula:
The differential external resolver carrier source type enables use of two analog input signals from the HIL/TyphoonSim (internal virtual IO bus in TyphoonSim) analog channels with the res_ai_pin_1 and the res_ai_pin_2 addresses. Analog signals from these HIL/TyphoonSim (internal virtual IO bus in TyphoonSim) analog inputs are subtracted, and the resulting signal is used as the external differential carrier source. Additionally, offset (V) and gain (V/V) values can be assigned to the input signal (similarly to the single ended case), according to the formula:
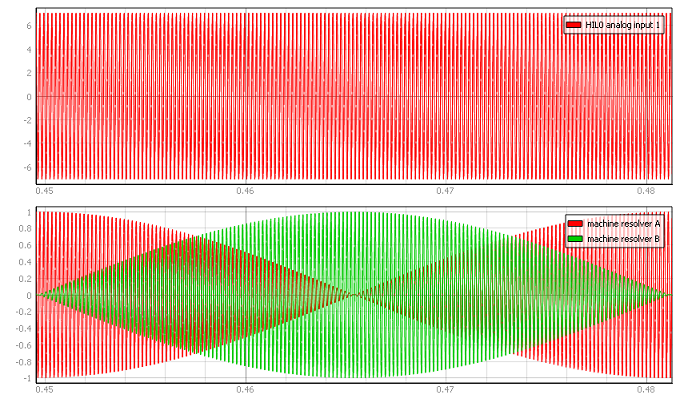
The following expression must hold in order to properly generate the encoder signals:
| symbol | description |
|---|---|
| enc_ppr | Encoder number of pulses per revolution |
| fm | Rotor mechanical frequency [Hz] |
| Ts | Simulation time step [s] |
Advanced (Tab)
- Theta_ab
- Position of the stationary αβ reference frame, in respect to the stator phase a axis [rad]
- Field Input
- Physical quantity applied to the field winding - voltage or current. It refers to the rotor-side.
In order for the input field current to be referred to the stator parameter, Ns/Nfd in the Electrical Tab should be set to
Note: If field input is defined as current, the field winding equation is removed from the mathematical model. Instead, the field input current is used as the model's input. There is no support for 2 q-axis damper windings with current input as of yet. For linear machine models, you can choose whether to apply voltage or current to the field winding. Nonlinear machine models only allows voltage as a field input.Field Input option is not supported in TyphoonSim. Changing its value will not affect TyphoonSim simulation at all
The machine model output variables (currents, voltages and fluxes) can be observed from a stationary reference frame. There are two widely used approaches in electrical machine modeling: in the first, the alpha axis of the stationary reference frame lags by 90 degrees in regard to the stator phase a axis (used by default, and indicated in a) Figure 5. In the second one, the alpha axis is aligned with the stator phase a axis (indicated in b) Figure 5. The user can select between these two situations.
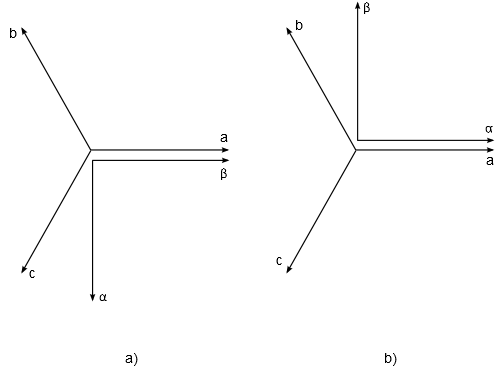
It is important to know the value of Theta_ab when the rotor position feedback is necessary. As an example, if a model uses the mechanical angle as a feedback signal and feeds it to one of the abc to dq, alpha beta to dq, dq to abc, or dq to alpha beta transformation blocks, the same transformation angle offset value should be used in both components to ensure the expected simulation results.
Snubber (Tab)
- Rsnb rotor
- Rotor snubber resistance value [Ω]
- Rsnb stator w1
- Stator winding 1 snubber resistance value [Ω]
- Rsnb stator w2
- Stator winding 2 snubber resistance value [Ω]
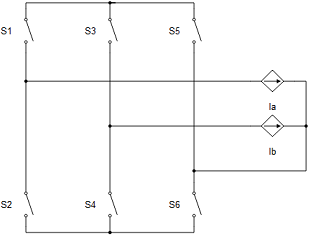
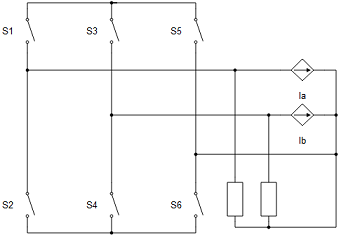
All machines with current source based circuit interfaces have the Snubber tab in the properties window where the value of snubber resistance can be set. Snubbers are necessary in the cases when an inverter or a contactor is directly connected to the machine terminals. This value can be set to infinite (inf), but it is not recommended when a machine is directly connected to the inverter since there will be a current source directly connected to an open switch. In this case, one of each switch pairs S1 and S2, S3 and S4, and S5 and S6 will be forced closed by the circuit solver in order to avoid the topological conflicts. On the other hand, with finite snubber values, there's always a path for the currents Ia and Ib, so all inverter switches can be open in this case. Circuit representations of this circuit without and with snubber resistors are shown in Figure 7 and Figure 8 respectively. Snubbers are connected across the current sources.
Output (Tab)
This block tab enables a single, vectorized signal output from the machine. The output vector contains selected machine mechanical and/or electrical variables in the same order as listed in this tab.
- Execution rate
- Signal processing output execution rate [s]
- Electrical torque
- Machine electrical torque [Nm]
- Mechanical speed
- Machine mechanical angular speed [rad/s]
- Mechanical angle
- Machine mechanical angle [rad]
- Stator 1 d-axis current
- Direct axis component of the stator 1 current [A]
- Stator 1 q-axis current
- Quadrature axis component of the stator 1 current [A]
- Stator 1 d-axis flux
- Direct axis component of the stator 1 flux [Wb]
- Stator 1 q-axis flux
- Quadrature axis component of the stator 1 flux [Wb]
- Stator 2 d-axis current
- Direct axis component of the stator 2 current [A]
- Stator 2 q-axis current
- Quadrature axis component of the stator 2 current [A]
- Stator 2 d-axis flux
- Direct axis component of the stator 2 flux [Wb]
- Stator 2 q-axis flux
- Quadrature axis component of the stator 2 flux [Wb]
Extras (Tab)
The Extras tab gives you the opportunity to set Signal Access Management for the component.
- Public - Components marked as public expose their signals on all levels.
- Protected - Components marked as protected will hide their signals to components outside of their first locked parent component.
- Inherit - Components marked as inherit will take the nearest parent 'signal_access' property value that is set to a value other than inherit.