Home
Typhoon HIL Software Manual
Schematic Editor Component Libraries
Detailed functionality and use of the pre-built Component Libraries in Schematic Editor
Component library
This section describes the general properties of the component library in Schematic Editor, and provides a list of main types of components available in it.
Transmission lines
This section describes the general properties of all transmission line components in Typhoon HIL's Schematic Editor. There are currently 3 different transmission line components in Schematic Editor.
Single phase Bergeron transmission line
This section describes Bergeron single phase transmission line based on a distributed parameter traveling wave model with lumped resistance.

Typhoon HIL Software Manual
- Introduction
  Overview of the categories covered in the Typhoon HIL Software Manual
- System Requirements
  Guidelines for the hardware and/or software environment necessary to run Typhoon HIL Control Center, for both PC and Test Server/Virtual Machine-based setups.
- Typhoon HIL Quick Start Guide
- Typhoon HIL Toolboxes
  List of the Toolbox Packages available in the Typhoon HIL software suite
- Connecting to your HIL device
  Guidelines on how to connect to a HIL device using either USB or Ethernet ports.
- Device Manager
  Device Manager is used to create, manipulate, and activate HIL device setups.
- Typhoon HIL Control Center
  This section provides a general description of Typhoon HIL Control Center and lists the main software components accessible from it, as well as additional software tools which can be invoked from its interface.
- Example Explorer
  General Description of the Typhoon HIL Control Center Example Explorer.
- Signal Access Management
  This feature allows you to change the visibility of signals in Schematic Editor and HIL SCADA
- Schematic Editor
  Introduction to the Schematic Editor tool in Typhoon HIL Control Center
- Schematic Editor Component Libraries
  Detailed functionality and use of the pre-built Component Libraries in Schematic Editor
  - Modeling principles
    This section describes modeling principles used in Typhoon HIL's software.
  - Model partitioning
    This section describes the general motivation and gives some practical guidelines for model partitioning.
  - Component library
    This section describes the general properties of the component library in Schematic Editor, and provides a list of main types of components available in it.
    - Circuit breakers
      This section describes the general properties of all circuit breaker components in Typhoon HIL Schematic Editor. There are currently 2 different circuit breaker components in Schematic Editor.
    - Communication
      Summary of the Communication components available in Schematic Editor.
    - Contactors
      This section describes the general properties of all contactor components in Typhoon HIL's Schematic Editor. There are currently 2 different contactor components in Schematic Editor.
    - Converters
      This section provided a general description of converters in Schematic Editor, including converter control options, thermal model, variable delay, and the Measurements tab.
    - Converters - extras
      This section describes additional components related to converter modeling.
    - HIL Interfaces
      This section describes the HIL Interface components in Typhoon HIL Schematic Editor.
    - Machines
      This section describes the concepts used in the modeling and implementation of electrical machine components in Typhoon HIL Schematic Editor. There are currently 26 different machine components.
    - Measurements
      This section describes measurement components in Schematic Editor, including voltage and current measurements and RMS measurements.
    - Microgrid
      This section describes the Microgrid library category in Typhoon HIL Schematic Editor.
    - Circuit partitioning components
      This section describes the general properties of circuit properties components in Typhoon HIL's Schematic Editor, such as core couplings, device couplings, core markers, device markers, etc.
    - PHIL Interfaces
      This section describes the general properties of Power Hardware-In-the-Loop (PHIL) interface components.
    - Passive components
      This section describes passive components, including linear passive components, nonlinear passive components and variable passive components.
    - Port components
      Description of the collection of Port components in Schematic Editor, which are used to connect internal subsystem elements to the outside schematic.
    - Signal processing components
      This section describes the general properties of all signal processing components in the Typhoon HIL Schematic Editor core library.
    - Interface components
      This section describes the general properties of all interface components in Typhoon HIL's Schematic Editor, such as voltage and current measurements, signal-controlled sources, contactors, etc. There are currently 4 different interface components in Schematic Editor.
    - Sources
      This section describes source components in Schematic Editor, including independent sources, controlled sources, externally controlled sources, signal controlled sources, batteries, photovoltaic panels, constant power loads/sources, and engine-generator sources.
    - System
      This section describes additional components in the System library in Schematic Editor
    - Test Suite
      This section describes the Test Suite components of Typhoon HIL's built in Schematic Editor Library, which currently includes the grid simulator, DC measurements, anti-islanding container, and grid fault components.
    - Transformers
      This section describes the general properties of all transformer components in Typhoon HIL's Schematic Editor, such as an ideal transformer, a single-phase three winding transformer, a three-phase four winding transformer, etc. There are currently 9 different transformer components in Schematic Editor.
    - Transmission lines
      This section describes the general properties of all transmission line components in Typhoon HIL's Schematic Editor. There are currently 3 different transmission line components in Schematic Editor.
      - RL section
        This section describes RL section
      - Transmission line
        This section describes transmission line
      - Underground cable
        This section describes underground cable
      - Single phase Bergeron transmission line
        This section describes Bergeron single phase transmission line based on a distributed parameter traveling wave model with lumped resistance.
      - Three phase Bergeron transmission line
        This section describes Bergeron three phase transmission line based on a distributed parameter traveling wave model with lumped resistance.
    - Component additional information
      This section describes the general properties of several components in Typhoon HIL's Schematic Editor whose feature set and capabilities require separate sections.
  - References
    This section describes references
- Third-party integrations
  This section provides an overview of the key third party integrations within Typhoon HIL's toolchain.
- HIL SCADA
  Description of the HIL SCADA tool in Typhoon HIL Control Center
- Waveform Generator
  This section describes the waveform generator tool in Typhoon HIL Control Center.
- Test and Calibration Tool
  Description of the Test and Calibration tool in Typhoon HIL Control Center
- TyphoonTest IDE
  This section describes TyphoonTest IDE
- Signal Analyzer
  This section describes the Signal Analyzer tool.
- Lookup table extraction tool
  Description of the Typhoon HIL Control Center tool for extracting characteristics (lookup tables) from datasheet graphs and charts into a format that can be imported by non-linear models.
- Package Manager
  Description of the Typhoon HIL Control Center tool for creating and managing Typhoon packages that contain Schematic examples, Schematic and widget libraries, documentation etc.
- Usage Logging
  This section briefly describes Typhoon HIL software logging feature.
- Python Interpreters
  Overview of how you can use Typhoon HIL Python Interpreters to further customize your test files.

Single phase Bergeron transmission line

This section describes Bergeron single phase transmission line based on a distributed parameter traveling wave model with lumped resistance.

Properties for this model are length of the line in kilometers, per length resistance in ohms/km, per length core and shield capacitance in farads/km, per length inductance in henries/km and execution rate in seconds.

Figure 1. Properties window of Bergeron single phase model

Figure 2. Symbol

Description

Figure 3. Model of the two-point lossless line

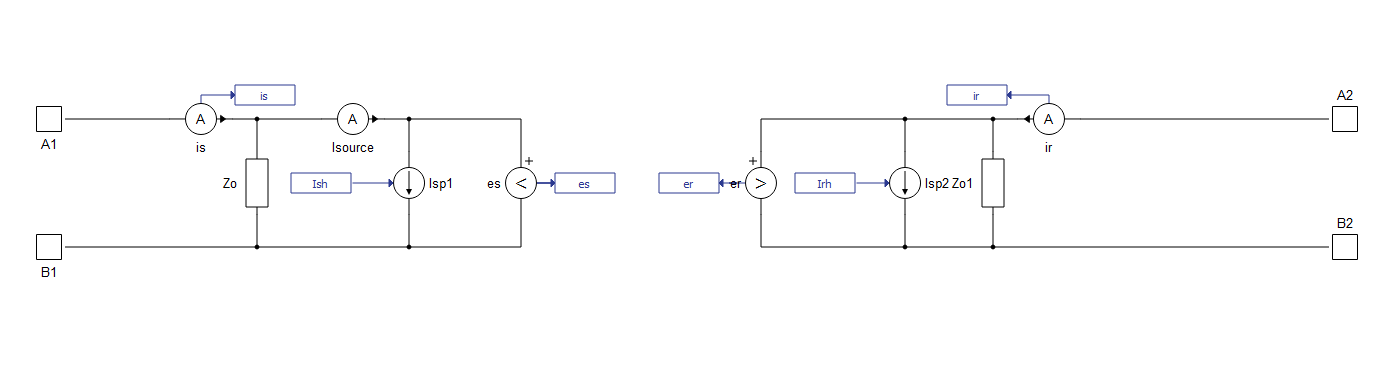
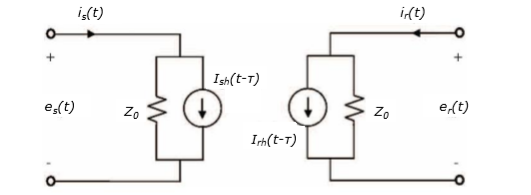
This model represents the L and C elements in a distributed manner while resistance R is lumped. In the case when line is lossless( r = 0), model is characterized by two values: the wave propagation speed $v = \frac{1}{\sqrt{l c}}$ and the characteristic impedance $Z_{o} = \sqrt{\frac{l}{c}}$ .

Transport delay is $τ = \frac{d}{v}$ , where d is the length of the line and v is the propagation speed.

It is important to note that transport delay value must be greater than execution rate.

The model equations are:

$i_{s} (t) = \frac{1}{Z_{o}} e_{s} (t) + I_{s h} (t)$

math $i_{r} (t) = \frac{1}{Z_{o}} e_{r} (t) + I_{r h} (t)$

And two current sources are:

$I_{s h} (t - τ) = - \frac{1}{Z_{o}} e_{r} (t - τ) - i_{r} (t - τ)$

$I_{r h} (t - τ) = - \frac{1}{Z_{o}} e_{s} (t - τ) - i_{s} (t - τ)$

This set of equations can be implemented for time discrete modelling of the line if the transport delay, τ, is integer multiple of the simulation step, T , or can be approximated as such: τ = NT.

For lossy lines, total resistance $R = r d$ is lumped, $\frac{1}{4}$ at each end and $\frac{1}{2}$ in the middle of the line. When losses are taken into account, equations are obtained as:

$i_{s} (t) = \frac{1}{Z} e_{s} (t) + I_{s h}^{'} (t - τ)$

$I_{s h}^{'} (t - τ) = \frac{\frac{R}{4}}{Z} [- \frac{1}{Z} e_{s} (t - τ) - \frac{Z_{0} - \frac{R}{4}}{Z} i_{s} (t - τ)] + \frac{Z_{0}}{Z} [- \frac{1}{Z} e_{r} (t - τ) - \frac{Z_{0} - \frac{R}{4}}{Z} i_{r} (t - τ)]$

$i_{r} (t) = \frac{1}{Z} e_{r} (t) + I_{r h}^{'} (t - τ)$

I_{r h}^{'} (t - τ) = \frac{\frac{R}{4}}{Z} [- \frac{1}{Z} e_{r} (t - τ) - \frac{Z_{0} - \frac{R}{4}}{Z} i_{r} (t - τ)] + \frac{Z_{0}}{Z} [- \frac{1}{Z} e_{s} (t - τ) - \frac{Z_{0} - \frac{R}{4}}{Z} i_{s} (t - τ)]

where:

$Z = Z_{o} + \frac{r d}{4}$

Figure 4. Schematic diagram of single phase Bergeron transmission line

References

[1] Dommel, H., “Digital Computer Solution of Electromagnetic Transients in Single and Multiple Networks,” IEEE® Transactions on Power Apparatus and Systems, Vol. PAS-88, No. 4, April, 1969.